Using monitoring data to derive and assess against guideline values
Before reading this page, you should read:
Assessing water quality condition against agreed water quality objectives is an essential part of managing our aquatic ecosystems. This assessment process may help to determine:
- improvements or declines in water quality
- any specific events or management interventions that caused changes to important water quality indicators.
Protection of the community values of waterways
Guideline values need to be set before water quality can be assessed. These values are numerical measures, such as concentrations, that support and maintain the community values of the water body.
You can derive guideline values for many physical and chemical (PC) stressors, sediment and water toxicants, and biological indicators.
Water quality objectives (agreed between water quality managers and the community) use guideline values and may reflect other considerations, such as the social or economic implications of an objective.
Usually, one or more water quality indicators (can be specified at the national level and applied fairly uniformly) are used to underpin a range of community values, including:
- primary industries requirements (e.g. aquaculture, stock watering)
- recreational use (e.g. swimming)
- human drinking-water supply.
Different guideline values for the same indicator may support or maintain different uses. For example, the requirements for stock use are more liberal than those for human drinking water.
Guideline values also vary across different types of water bodies, such as upland streams and estuaries.
The national guideline values are typically taken as the default guideline values (DGVs) in the absence of more appropriate local information.
General approach for aquatic ecosystems
Aquatic ecosystems are complex and heterogeneous, and it is often essential to reflect local condition in the guideline values.
Guideline values for each of the lines of evidence associated with stressors and ecosystem receptors for aquatic ecosystems may be derived using:
- reference-site data, or
- biological-effects data (e.g. toxicity data).
Available reference-site data
A referential approach is commonly used to derive locally relevant water quality guideline values, particularly for PC stressors, toxicants where background concentrations naturally exceed DGVs and ecosystem receptors.
In this approach, the natural range of values for key indicators at reference sites is used to provide a suitable baseline for comparison against values derived from similar aquatic ecosystems. Ideal reference sites are similar to assessment sites (e.g. similar climate, relief and geology) but are minimally impacted, have limited exposure to anthropogenic drivers, and have sufficient historical data to characterise water quality condition and variability.
For modified ecosystems, ‘best available’ reference sites may provide the only choice for the reference condition. If the test or assessment site departs in a meaningful way from the condition of the reference site or designated reference condition, then that site is assessed to be affected in some way. (The ecological importance of such a departure can only be assessed with local information gathered for key ecosystem receptors in a weight-of-evidence evaluation.)
No available reference-site data
If no appropriate reference data are available at the outset, then it may be necessary to start with DGVs while data are being collected.
Sometimes surrogates may be used as true reference sites. Those sites may be from adjacent catchments or contain some level of impairment. In each case, it is critical to clearly understand what that site represents and the implications for any subsequent comparison with assessment sites.
Local guideline values may also be appropriate to specific conditions (e.g. low to moderate streamflow) or certain times of the year (e.g. wet season only) rather than the full year. Where possible, guideline values should respond to such specific factors but need to do so with the broader water quality objectives in mind.
For example, are we required to manage across the entire year even if departures in water quality are only ever likely early in the wet season? (Refer to Deriving and testing flow-based guideline values.)
Percentiles of concentration values
Where guideline values are derived from reference data, a percentile of concentration values of a suitable reference condition is typically selected for chemical and physical lines of evidence (in waters and sediment).
By default, the median quality values of freshwater and marine waters should be lower than the 80th percentile of concentration values of a suitable reference site (or above the 20th percentile for parameters such as dissolved oxygen where low values are the problem).
For ecosystem receptors, percentiles or other statistical measures of change from a reference condition also serve as guideline values, although this (guideline) term may be more commonly referred to as the ‘effect size’ (refer to Assessment of change through data analysis).
In general, the more the guideline value reflects — or is perceived to reflect — actual biological change (e.g. ecosystem receptors, or stressor concentrations approaching values that may elicit harmful effects), the smaller would be the change from central tendency in the reference condition used to define the guideline value, and the smaller the ‘allowable’ or acceptable deviation from the guideline value in assessing water quality condition against the guideline value.
This more conservative principle of guideline assessment also applies to chemical and physical lines of evidence in waters and sediment for which guideline values are based on biological-effects data (DGVs or locally derived site-specific guideline values).
In such cases, you should apply a more conservative approach to the comparison of toxicant-test data with DGVs. Specifically, we recommend that a toxicant DGV is deemed to be exceeded if the 95th percentile of the test distribution exceeds the DGV (or stated differently, there has been no exceedance of the DGV if 95% of the values fall below the DGV).
The more stringent approach is recommended here because, unlike PC stressors, toxicant DGVs are based on actual biological-effects data and so, by implication, exceedance of the value indicates the potential for ecological harm. The proportion of values required to be less than the DGV is very high (95%) so a single observation greater than the DGV would be legitimate grounds for determining that an exceedance has occurred in most cases, even early in a sampling program.
Estimation of percentiles from data
The estimation of local guideline values for a reference site typically relies on the estimation of a percentile from the historical data at that reference site.
There is no one correct way to estimate percentiles (Hyndman & Fan 1996, McBride 2005, Schoonjans et al. 2011). The New Zealand Ministry for the Environment recommended the Hazen percentile estimator as a middle-of-the-road estimator (MfE 2003). Many different methods are available in statistical software and the difference between different estimators will typically be small.
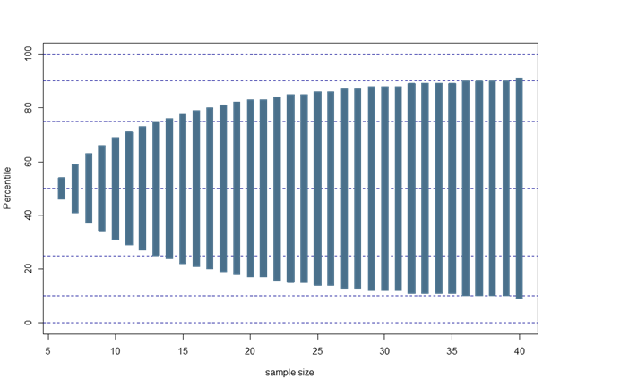
The precision with which the percentile is estimated depends heavily on the sample size.
Figure 8 presents the percentiles that may be estimated, with 95% error bounds as a function of sample size. The error bounds are derived using a binomial nonparametric confidence interval. The figure indicates that we need at least 13 samples to estimate a 25th or 75th percentile with an associated 95% confidence interval. To estimate the 10th or 90th percentile, the sample size would increase to a minimum of 36.
Larger sample sizes are required to estimate extreme percentiles.
Similar performance would be expected from estimating percentiles with uncertainty bounds for a given sample size using nonparametric bootstrap estimation. Parametric intervals may be narrower, enabling estimation of extreme percentiles with smaller sample sizes but this may depend on the validity of the assumed distributional form.
The implication here is that less extreme percentiles may be estimated with smaller sample sizes. If only small samples sizes are practically or logistically feasible, then it may sometimes make more sense to adjust the percentiles.
Data collected over time are typically serially correlated, with observations that are closer in time being more likely to be similar.
Positive autocorrelation has the effect of reducing our effective sample size and underestimating the uncertainty. Esterby (1989) noted that it was often possible to space observations far enough apart, or aggregate them by taking means or medians, to reduce any dependence.
While many statistical analysis methods assume independent data, variants for correlated data often exist and may need to be explored.
Small sample sizes
If there are limitations to the number of samples that are available for the test conditions (e.g. quarterly data are available rather than monthly data), then you have several options to consider. These considerations are as relevant to deriving guideline values as they are for assessing against guideline values because both seek to estimate percentiles or particular quantities from the monitoring data.
The sample size may be increased in some circumstances by pooling data across time or space.
From a temporal perspective, data may be pooled across a longer time period. For example, data collected over a 2-year window may be used rather than a 1-year window. This may be implemented on a rotational basis, much like a moving average, where only the most recent 2 years (or whatever agreed window) is used to estimate the current or reference condition to improve the precision.
From a spatial perspective, it may be sensible to consider multiple locations and pool data from more than one site to increase the sample size.
In all cases, it is essential to carefully consider and communicate the sources of variation and the representativeness of the data for making inferences about the water body (or part of the water body) of interest.
For instance, pooling data across more than one site rather than across multiple seasons for either the estimation of reference/guideline or current condition may mean that the data underrepresents the seasonal variation, which may be a substantial source of the variation in condition, and could potentially lead to misleading inferences.
As another example, if there is interest from a compliance perspective in the plume from a wastewater discharge, then it may make sense to choose a subset of sites in the mixing zone to define guideline values relevant for assessing discharge against. Or, if more than one site is combined, then you could simply pool the data or pool the summary statistics.
Clear rules and transparency need to underpin the approach taken so as to minimise any ambiguity surrounding the inferences or implications.
When samples sizes are small, it may be sensible to consider parametric approaches that generally have more power than nonparametric approaches, although at the cost of being more sensitive to departures from assumptions. McBride (2003) compared parametric and nonparametric approaches.
Condition assessment against guideline values
Here we focus on statistical approaches for assessing condition based on monitoring data against a guideline value for a given water quality variable.
We consider the approaches designed to compare the current status with an estimate of the system under reference condition. If the current status is not seen as stable, whether the system be in reference condition or not, then it may be more appropriate to start by examining the data for trends in water quality.
The primary statistical methods are for percentile-based water quality objectives.
We acknowledge that water quality objectives may be considered much more generally. For instance, you may be interested in the time between events of a certain magnitude, or in the duration of time that water quality exceeds a specific guideline value because that may have larger ecosystem health implications than a larger number of isolated exceedances.
While framed within a ‘compliance’ setting, we strongly encourage you to interrogate and question the data and modelling assumptions. Focus on discovering and understanding the spatial and temporal dynamics of an environmental effect, instead of on finding, for example, that the control and affected sites differ.
Testing hypotheses, decision errors and the burden of proof
Use your collected monitoring data to assess the condition of the water body relative to the water quality objectives or guideline values.
A water body is typically considered to attain a water quality guideline value if there is no evidence to the contrary. Non-attainment results from exceeding the water quality guideline values in some way and may be specified in terms of the:
- frequency of the exceedances
- duration of the exceedances, or
- magnitude of the exceedances.
The direction of ‘exceedance’ depends on the context, which can be above or below the water quality guideline values according to what constitutes greater impairment. For example, higher concentrations of nutrients or lower concentrations of dissolved oxygen may both signify greater ecosystem impairment.
Exceedances may relate to individual transient changes in condition, possibly related to unusual circumstances (e.g. a large inflow event), or they may represent a fundamental shift in the distribution of water quality that is persistent and ongoing.
When the time of the change is known (e.g. after some specific management intervention) and the focus is on detecting whether this leads to a noticeable effect on the ecosystem, before–after, control–impact (BACI) designs may be useful in detecting between the condition ‘before’ and ‘after’.
Here we primarily focus on situations when the ‘when’ is not known, or when there has been a transient or persistent change. This ‘surveillance mode’ uses statistical methods to assess when or if there has been a change.
It is important that the sampling variability is acknowledged in both setting guideline values and assessing attainment against them so that any conclusions that are reached refer to the entire water body and not just the sample collected. Uncertainties need to be considered in setting water quality objectives and assessing attainment (Barnett & O’Hagan 1997).
Condition assessments use data from a monitoring program — possibly purposely designed — to decide whether a water body (e.g. a stream, lake or estuary) attains a prescribed water quality guideline value. This is a statistical decision problem where the sample data are used to make an inference about the true condition of the water body.
A decision on attainment can result in (Table 1):
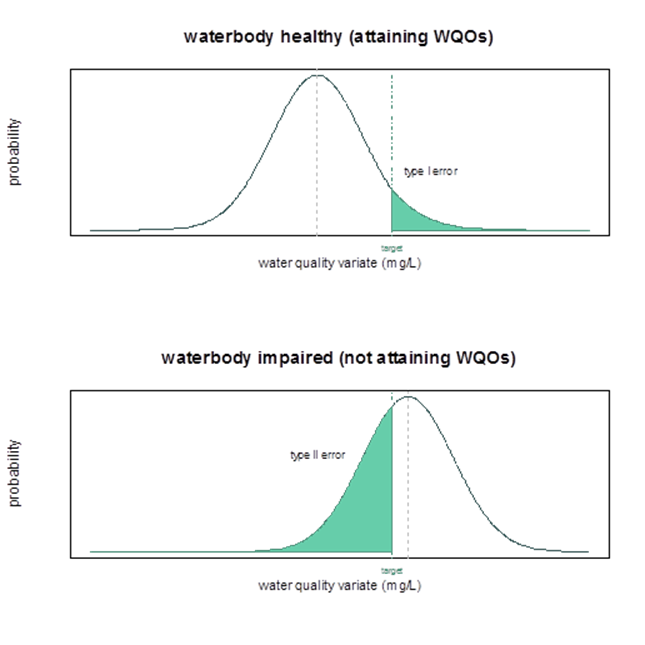
- a Type I error — probability of wrongly declaring non-attainment when in fact the water body attains the guideline value (false positive)
- a Type II error — probability of incorrectly declaring attainment with the water quality guideline value when in fact the water body does not attain it (false negative).
| True state of nature | Decide attainment | Decide non-attainment |
|---|---|---|
| True attainment (H0 true) | Correct value | Type I error |
| True non-attainment (H0 false) | Type II error | Correct value |
There is a fundamental trade-off between these 2 decision errors.
Consider the target in Figure 2, which is set to detect large values of the water quality variate and shows the Type I and Type II error rates for a specific alternative. If the target value was set higher, then this would reduce the Type I error (top chart in Figure 2) because there would be a lower probability that a water body in attainment would exceed the target. This would however be at the expense of a higher Type II error rate (bottom chart in Figure 2) because we would be less able to detect when the water body is not attaining the desired water quality standard.
This simple representation extends to a fuller consideration of statistical power, which is the probability that a true deviation from the null hypothesis will be detected (Fairweather 1991).
The sample size available to assess the condition of the water body can strongly affect these error rates.
For small sample sizes, it is harder to detect non-attainment. As the sample size increases, and for a fixed Type I error, fewer Type II errors will be made because the larger sample sizes enable detection of a given non-attainment more readily. The Type I error rate, Type II error rate and the sample size are intimately linked. If two are set or known, the third is determined.
It follows that if we set a confidence level or Type I error rate and have a fixed sample size, then our ability to detect a difference of a given magnitude is determined. Or, if we need to specify the Type I and Type II error rates directly, then this will inform the minimum sample size required.
Careful choice of the confidence level and the sample size will ensure a reasonable balance between these error rates (Gibbons 2003).
The decision rule in the environmental setting must balance the competing interests of:
- risk for regulators — that an impaired water body is deemed to have met the water quality objectives (Type II error)
- risk for industry — that a healthy water body is not found to meet the water quality objectives (Type I error).
The burden of proof relates to who receives the benefit of the doubt and who has to bear that cost, whether that is financial or forgone uses, for any error. The burden of proof should be considered explicitly.
The null hypothesis assigns some benefit of doubt. While the null hypothesis is never accepted, to reject it there must be enough evidence to support the alternative hypothesis.
The decision on what to assume as the null hypothesis is an important one and needs to balance the risks and costs of the respective errors.
Currently, if the site is considered impaired or to be of condition outside the water quality objectives, then it is necessary to provide evidence that the water body is healthy or in attainment. On the other hand, if the site is considered healthy, it will stay that way until evidence exists to change that assessment.
It is essential to know what size of change the monitoring program needs to be able to detect with high probability. This is difficult to determine but has key implications for the number of samples that need to be collected and the trade-off between the Type I and Type II error rates — and their respective costs — that must be managed.
While the specification of the effect size is often up for debate and difficult to make ecologically meaningful, it is important to focus on changes that are of ecological significance wherever possible because they are the changes that a water quality monitoring program needs to be able to detect.
In practice, for a given water quality objective, the error rates stem directly from the distribution of the water quality variable, whether that be the historical distribution or the distribution under change. The error rates are not directly related to the objective-setting process.
Choosing a method for assessing condition against water quality objectives
Here we consider methods for assessing condition against water quality objectives. This concentrates on retrospective assessments, where observed water quality data over a period of time (e.g. monthly data over a 12-month period) have been collected and it is necessary to make an assessment.
There are 2 broad approaches for doing this:
- Methods that collapse time and treat the data as a sample from a distribution, with no specific interest in the time order
- Methods that account for time directly and consider the time order in any assessment.
Methods that consider data as a sample from a distribution
When data are observed over a period of time and an assessment is made over that period, it can be done without explicit reference to the time order. These methods are generally based on:
- number of exceedances of the target, or
- comparison of some distributional quantity (e.g. mean, 80th percentile) to its target — particularly useful when the magnitude of the exceedance is important.
Observed percentiles
Rules are based on the observed or empirical percentiles and number of exceedances of the target or guideline value. For example, if the proportion of exceedances is greater than 20%, then the water body is assessed to be not in attainment. The ANZECC & ARMCANZ (2000) guidelines trigger approach is an example of this type of rule.
The use of observed percentiles is based on the sample data and does not make any inference about whether the ‘population’ is in attainment because it does not consider confidence intervals. The population in this context is defined as that part of the water body for which an assessment is required. It requires a clear and precise definition of the resource.
The target population is the collection of elements about which information is wanted (Cochran 1987, Särndal et al. 1992). In practice, the target population is accessed through a sampling frame. This is a construct (e.g. a list) that provides observational access to the population elements. In cases where a routine number of samples may be collected consistently (e.g. monthly data), the error rates will be consistent and is therefore less of an issue over time. This assumption underpins the ANZECC & ARMCANZ (2000) guidelines trigger approach because it is expected that the calculation of the median for the test data is based on a similar number of samples. The more samples used, the more accurately that median is estimated.
In general though, this approach does not control the error rates and can give unacceptably large Type I errors and falsely declare non-attainment with the water quality guideline values (Gibbons 2003, Shabman & Smith 2003, Smith et al. 2003).
While the error rate does depend on the sample size, the observed percentiles approach does not explicitly consider the risks and costs of making a decision error. The error rates are also discrete and can change quite sharply.
For instance, when n = 12, which might correspond to monthly sampling of a water body, 1 sample is allowed to exceed the water quality standard and still be considered to be in attainment under a ‘10% rule’. The same is true up until n = 20, when 2 samples are allowed to exceed the standard but maintain attainment. For smaller sample sizes, there is less certainty that the observed sample proportion is showing attainment or non-attainment by chance.
Percentile confidence intervals
The binomial approach uses the same data as the observed percentiles approach. It treats the exceedance of the target as a binary outcome, where an exceedance is assigned the value 1 and a non-exceedance is assigned the value 0. Assuming n independent monitoring times (trials), the number of exceedances may be treated as a binomial random variable with parameters n and probability of exceedance p.
Under the null hypothesis of attainment, there is a known (at least approximately from historical data) probability of exceeding the water quality guideline value, where:
H0: p ≤ 0.05 (in attainment).
If there is some impairment of the water body, then the probability of exceedance will be greater than 0.05 so that the alternative hypothesis is:
H1: p > 0.05
The binomial approach to assessing attainment with the water quality guideline value is to assess if there is sufficient evidence from that sample data to reject the null hypothesis.
For a sample size n, the decision will determine a cut-off in terms of the number of exceedances so that the probability of falsely adjudging non-attainment when the water body is actually unimpaired is less than the desired Type I error rate.
It is common practice to set the Type I error rates to be 0.05 or 0.10 and to control the Type II error through the sample size (Smith et al. 2001).
Relative to the raw score approach, it is susceptible to larger Type II errors, although these may be managed more effectively because it is possible to trade between the 2 errors and incorporate the effect of the sample size.
The binomial approach is popular because it does not make any distributional assumptions in assessing attainment and it offers the ability to control the error rates. However, it does not use any information about the magnitude of the departures — only whether or not the target was exceeded.
Example of calculating binomial probability
For toxicants, it is recommended that action is triggered if the 95th percentile of the test data exceeds the guideline value.
Suppose the 95th percentile of cadmium (Cd) data for marine waters is not to exceed 5.5 μg/L. At one location, 5 water samples have the Cd measurements (μg/L): 4.6, 4.4, 5.6, 4.7, 4.1.
Assuming that the 95th percentile for Cd in the marine waters is equal to 5.5 μg/L, then it can be seen that there is a 5% chance that a single reading will exceed this level.
When n independent readings are taken, the probability of the number of samples r exceeding the guideline value can be obtained from the binomial probability distribution. In this case, with n = 5 and p = 0.05.
Probability that r out of 5 samples have Cd > 5.5 μg/L =
To compute a p-value for assessing the significance of our sample result, the probabilities of this event (and more extreme events) are computed and summed. In this case:
Prob.(1 exceedance) + Prob.(2 exceedances) + … + Prob.(5 exceedances)
= 1 – Prob.(0 exceedances)
= 1 –
= 1 – 0.955
= 0.226
This probability is much greater than the conventional 0.05 level of significance so there is insufficient evidence to assert that the guideline has been breached. In other words, it is quite probable that at least 1 out of 5 readings will exceed the 95th percentile. This statement holds true irrespective of the actual numerical value of the 95th percentile or the distribution of readings.
Most statistical software can calculate binomial probabilities.
The Bayesian binomial approach (McBride & Ellis 2000, Smith et al. 2001) extends the binomial approach by incorporating additional information about the probability of an exceedance into the prior information. This treats the probability of impairment as a random variable that has an associated distribution.
Additional information about this distribution that is available before the sample is taken, which may come from past data or from nearby sites that are similar, can be used to formulate a prior distribution. The Bayesian paradigm is then used to combine the prior information and the monitoring data to summarise the knowledge about the probability of impairment in terms of a posterior distribution. It follows that sites with less history of impairment will require more exceedances to be assessed as not in attainment with the water quality guideline values.
Bayesian approaches may also allow other information and knowledge sources to be incorporated into the condition assessment. This information could come from historical records, related sites or other sources, including expert opinion.
Confidence intervals for population characteristics
This approach calculates a confidence interval for the true percentile of the distribution.
If the confidence interval is found to exceed the water quality guideline value, then the water body is assessed as not in attainment.
If the entire confidence interval falls within the water quality guideline value, then the water body is within attainment.
If the interval straddles the water quality standard, a conclusion will depend on the burden of proof and will require other considerations.
This approach is based on a confidence interval so it accounts for uncertainty and is superior to simply using the observed percentiles. Goudey (2007), an advocate of this 3-way decision process, suggested that it could provide more sensible feedback for environmental decision-making.
Several procedures are available for computing a confidence limit for a percentile of a distribution.
Gibbons (2003) described confidence limits based on a normal distribution, confidence limits based on a log-normal distribution, and nonparametric confidence limits that appeal to the binomial distribution.
An alternative empirically driven approach would be to use bootstrap resampling to produce a confidence interval for a given percentile. The effectiveness of the bootstrap will depend on the sample size and the percentile. Larger sample sizes will be necessary for more extreme percentiles. Bootstrap is also computationally more demanding than explicit parametric approaches.
Acceptance sampling
Acceptance sampling by variables is a popular approach in statistical quality control that makes an assessment about attainment on the basis of some function of the measurements rather than the number of samples exceeding the water quality target.
Since it makes use of the actual values, and therefore the magnitude of any exceedances, acceptance sampling uses more of the available information and can require smaller sample sizes for a given error rate. However, it needs assumptions to be made about the distributional form.
You can assess attainment using acceptance sampling by:
- Calculating the probability of exceeding the water quality target, given the observed data and assumed probability distribution, and determining if that probability is greater than the allowable probability of impairment.
- Calculating a critical value for the sample mean (or another parameter of interest) that corresponds with exceeding the water quality standard for a specified level of confidence. The decision rule then involves comparing the observed sample mean to this value.
Acceptance sampling has primarily been considered for normal and log-normal distributions. Smith et al. (2003) described it in detail in the context of water quality monitoring.
Factors that influence choice of method
Deciding what method and decision rule to use requires careful evaluation of the advantages and disadvantages of respective methods.
Ultimately, it is important to choose the method that extracts the most information about the condition of the water body from your data. This is particularly true when there are small sample sizes because there may be a greater need for more sophisticated statistical methods to make up for the lack of data support wherever possible.
It is often necessary to borrow strength from other data and information sources (e.g. other locations in the catchment). You may be able to pool information to produce background location and variation estimates. Bayesian approaches may be useful for bringing these different sources of information together so you can make a decision based on all the available information.
Statistical approaches may give benefit of doubt to the ‘polluter’ and not be sensitive enough to departures from attainment. This occurs because we typically assume that the water body complies with the water quality guideline values and then seek evidence to reject that hypothesis. The burden of proof is thus on demonstrating impairment (as opposed to assuming impairment and demonstrating attainment).
Unless there is a prior basis for assuming non-attainment or impairment, it is appropriate to assume a null hypothesis that the site is not impaired (Shabman & Smith 2003).
It is always important to be aware of the Type I and Type II error rates, and keep their associated consequences in mind. For Type II error rates, it is important to know a level of non-attainment or exceedances that the attainment monitoring program should be able to detect with high probability. It provides an important point of focus and makes it clear whether or not the program is receiving an appropriate level of resources to satisfy its objectives.
The monitoring program may have limited value if it has little power to detect a sizable departure from the water quality guideline values. Adopt methods that allow you to control the detection error rates, with the trade-off between them ultimately a risk management decision that should be based on the explicit consideration of the costs of the consequences of being wrong (Smith et al. 2001).
The binomial percent exceedance approach offers the ability to manage error rates, although in a discrete way. It is robust to the distributional form and can routinely handle below detection limit (BDL) data because all data are reduced to a binary outcome: meet or exceed. The main criticism of the binomial approach is that it does not make use of all the available information. By reducing the data to exceedances, for a target of 5.0 mg/L, we are treating a measurement of 5.1 mg/L the same as a measurement of 51.0 mg/L.
Approaches based on all the data look for changes in population parameters, such as the mean or distributional percentiles, by comparing confidence intervals for these characteristics to the agreed water quality objectives. These confidence intervals are obtained by appealing to:
- parametric distributional forms (e.g. normal, log-normal), or
- nonparametric methods (bootstrap or binomial nonparametric confidence intervals).
By using the actual data, we make use of all the available information and have more power to detect any change or departure (Esterby 1989, Gibbons 2003, Shabman & Smith 2003, Smith et al. 2003). Equivalently, fewer monitoring samples may be required to assess the performance against the water quality objectives with the same statistical power.
For the parametric approaches, the key challenge is that misleading confidence intervals may result from poorly specified or understood distributions. Confidence intervals are also only generally available for normal or log-normal data.
Gibbons (2003) noted that the nonparametric method has the advantage that it makes no distributional assumptions, and that this may be important for small sample sizes where there is naturally less certainty about the distributional form. However, confidence limits based on the normal distribution are noted as being fairly robust to distributional misspecification and can be used with reasonable confidence.
Chakraborti & Li (2007) noted that the nonparametric confidence interval based on the binomial distribution is generally wider than the explicit parametric approach, particularly for smaller sample sizes. When the distributions are well characterised, the nonparametric approaches are less efficient than their parametric counterparts.
Confidence intervals for percentiles or means are possibly easier to communicate than error rates based on the number of exceedances. Walshe et al. (2007), in a forestry context, were advocates of confidence intervals for assessing performance against forest management standards because the confidence interval communicates the key elements of effect size and the uncertainty associated with sampling and measurement error. The confidence intervals also contain key information about the statistical power and p-values but are not bound to the dichotomous outcome.
Methods that consider the time sequence
Alternative methodologies, such as control charts and water quality trend analyses, may provide a way of assessing a change more quickly. These methods focus on the time series and the nature of any exceedances. This may be important because a run of exceedances may have more serious implications for the ecological health of an aquatic ecosystem than an equivalent number of temporally isolated cases.
Statistical control charts may be a useful way of visualising attainment and checking data quality. It is possible to track individual values, means, standard deviations and proportions exceeding particular values at a variety of time scales. Some statistical tests can detect changes and other features, such as trends or periodicities, in control charts. By using actual data, control charts reduce the emphasis on exceedances and encourage the adoption of a risk-based approach. These charts make it possible to visually identify anomalies and to consider when the departures or exceedances occur. This may be important because clusters of non-attainment may have different implications for a number of isolated cases.
Control chart approaches that may be used to assess condition against water quality objectives include:
- cumulative sum (CUSUM) charts
- exponentially weighted moving averages (EWMAs)
- Shewart control charts.
Control charts are particularly valuable for detecting departures of quality from conditions meeting the water quality objectives. These departures may be short term and transient, or they may constitute a persistent and long-term shift in water quality.
EWMAs and CUSUM charts are typically used for assessing persistent shifts in water quality. Mac Nally & Hart (1997) used CUSUM charts to monitor environmental variables and attainment conditions. In reasonably buffered systems, they found that the CUSUM technique may be useful for detecting changes quickly.
Shewart control charts enable the detection of individual or short-term departures in water quality.
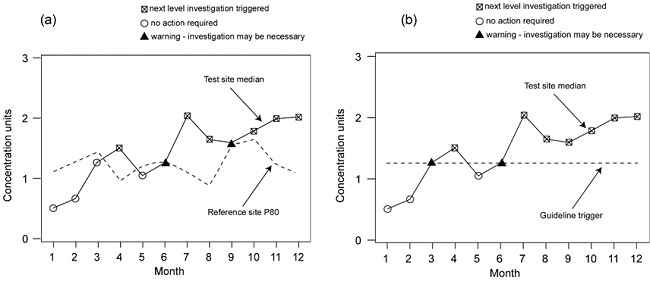
Monthly results for a test water body graphed in a control chart may look like:
- Figure 3(a) — compared to a guideline value obtained using the 80th percentile from reference-site monitoring, or
- Figure 3(b) —compared to a single published guideline value.
Confidence limits can be added to each of the plotted points when sample means are used but this is not straightforward when dealing with percentiles (particularly a ‘rolling’ percentile at a reference site).
Control charts have been used to routinely track and ensure quality in industrial processes. Part of their popularity derives from their strong visual depictions of condition, capacity to readily update and ease of communication, while still offering an ability to detect change. They are particularly useful for fairly stable ecosystem processes that are not subject to high variability and large changes in condition as part of the natural variation.
Where known sources of variation exist, control charts may be constructed so they present departures after adjusting for those known factors (e.g. seasonal variation).
Control charts are useful for detecting departures from the current condition so they work well when the focus is on protecting a healthy aquatic ecosystem by determining any evidence of non-attainment, either short-term or persistent shift changes. They are useful if the water quality objectives are not met and the focus is on determining progress towards meeting them but ultimately, when the objectives are met, the control chart may be less useful.
Examples of setting and testing against guideline values
Comparing test data with guideline values (ANZECC & ARMCANZ 2000)
Physical and chemical stressors
A trigger for further investigation of the test water body will be deemed to have occurred when the median concentration of a particular measurement parameter in n independent samples taken at the test water body exceeds the 80th percentile (or is below the 20th percentile if ‘less is worse’) of the same measurement parameter at the reference site.
A minimum of 2 years of consecutive monthly data at the reference site is required before a valid guideline value can be established based on that site’s percentiles. If this requirement has not been satisfied, then the median of the data values measured at the test site should be compared to the appropriate DGVs identified in the Water Quality Guidelines.
This rule is statistically based and acknowledges natural background variation by comparison to a reference site. Its robustness derives from the fact that it accommodates site-specific anomalies and uses a robust statistical measure as the basis for triggering. No assumptions are required to be made about the distributional properties of the data obtained from either the test or reference sites. The computational requirements of the approach are minimal and can be performed without the need for statistical tables, formulas or computer software.
Exceedances of the guideline values are intended as an ‘early warning’ mechanism to alert managers of a potential problem. They are not intended to be an instrument to assess ‘compliance’ and should not be used in this capacity.
The trigger protocol is responsive to shifts in the location (‘average’) of the distribution of values at the test site. Differences in shape of the reference and test distributions may sometimes be important but this is a secondary consideration that is not specifically addressed by this protocol.
The role of the 80th percentile at the reference site is to quantify the notion of a ‘measurable perturbation’ at the test site. The protocol is not a statistical test of the equivalence of the 50th and 80th percentiles.
Using a percentile of the reference distribution avoids the need to specify an absolute quantity. Another advantage is that the trigger criterion is being constantly updated to reflect temporal trends and the effects of extraneous factors (e.g. climate variability, seasonality) because the reference site is being monitored over time.
Implementation of the trigger criterion is both flexible and adaptive. For example, you can identify a level of routine sampling (through the specification of the sample size n) that provides an acceptable balance between the cost of sampling and analysis and the risk of false triggering.
The trigger criterion method encourages the establishment and maintenance of long-term reference monitoring as an alternative to comparisons with the DGVs that do not account for site-specific anomalies.
Before implementing the trigger rule, you will need to identify suitable reference sites and obtain data to characterise that site. The protocol recommends that 2 years of continuous monthly data at the reference site is required before a valid guideline value can be established. If not available, comparison of the test site median should be made with reference to the DGVs.
You can compute the 80th percentile at the reference site, which is always based on the most recent 24 monthly observations, by:
- arranging the 24 data values in ascending order (lowest to highest)
- taking the simple average (mean) of the 19th and 20th observations in the ordered set.
Each month, new readings at the reference and test sites are obtained. The reference-site observation is appended to the end of the original (unsorted) time sequence and the 80th percentile is calculated based on the most recent 24 data values.
Although only the most recent 2 years of data are used in the computations, all data should be maintained because it will allow you to compute longer-term statistics and may be useful for identifying trends.
This method provides you with flexibility for the allocation of resources to the sampling effort because there is no fixed requirement to monitor at a reference location (the DGVs can be applied). Similarly, the choice of sample size at the test site is arbitrary although there are implications for the rate of false triggering (Type I errors).
For example, a minimum resource allocation would set n = 1 for the number of samples to be collected each month from the test site. It is clear that the chance of a single observation from the test site exceeding the 80th percentile of a reference distribution, which is identical to the test distribution, is precisely 20%. Thus the Type I error in this case is 20%. This percentage can be reduced by increasing n. When n = 5, the Type I error rate is approximately 0.05. The concomitant advantage of larger sample sizes is the reduction in the Type II error rate.
The median is defined to be the ‘middle’ value in a set of data such that half the observations have values numerically greater than the median and half have values numerically less than the median. For small datasets, the sample median is obtained as either the single middle value after sorting in ascending order when n is odd, or the average of the two middle observations when n is even.
The proposed trigger rule does not purport to define or represent an ecologically important change. The trigger approach is an early warning mechanism to alert the resource manager of a potential or emerging change that should be followed up. Whether or not the actual change in condition at the test site has biological or ecological ramifications can only be ascertained by a much more comprehensive investigation and analysis.
To make this distinction clear, the concept of a measurable perturbation is introduced. The de facto definition of a measurable perturbation is the magnitude of the shift between the 50th and 80th percentiles at a reference site. While this definition is arbitrary, it does have broad acceptance and intuitive appeal among experts. The statistical significance associated with a change in condition equal to or greater than a measurable perturbation would require a separate analysis.
It is important that the statistical performance characteristics of any test or decision-making rule are documented and understood to avoid unduly conservative or liberal triggering. The foregoing discussion makes no assumptions regarding the shape of the reference and test distributions. Without this knowledge, a formal calculation of Type I and Type II errors is not possible. However, as a general principle, increasing the frequency of collection of independent samples will reduce the magnitude of both errors.
Visual inspection of all results may assist with month-by-month comparisons and help you to identify trends, anomalies, periodicities and other phenomena.
In the absence of suitable reference-site data, compare the median of the test-site data with the DGVs. The DGV has been computed as the 80th percentile of the amalgamation of a number of historical datasets across broad geographical regions. Unlike a comparison with a locally derived 80th percentile, the DGV is static and will not reflect any local spatial or temporal anomalies.
We strongly advocate for reference-site monitoring if these effects are considered to represent a significant source of departure from the DGV. Figure 3b illustrates the difference in control charting procedures when the DGV is used in place of a trigger obtained using the 80th percentile from reference-site monitoring.
Toxicants
Here we describe the general needs for comparing toxicant-test data with guideline values.
Conceptually, toxicants and PC stressors are subcategories of the same class of potentially hazardous indicators, being properties or (usually) constituents of the aquatic environment but for guideline purposes they are treated differently:
- Toxicants are usually compared with a single DGV, derived from a comprehensive set of available ecotoxicological data, and less commonly with a background or reference distribution.
- PC stressors at a test site are usually compared with those at a reference site (which has its parallels in measurement programs for toxicants).
Some natural surface waters will contain concentrations of toxicants that may exceed the DGVs. If this is the case, then new values should be based on background (or baseline) data. (In this case, ‘background’ refers to natural toxicant concentrations that are unrelated to human disturbance.) As a matter of course, gathering background data is always recommended, at least in the initial stages of a water quality management program, to establish whether or not concentrations of toxicants are naturally high.
Toxicant concentrations may vary seasonally. Because of this and the need to be confident about the best estimate of background concentrations, we recommend that background data be gathered on a monthly basis for at least 2 years. In all respects, data requirements and collection are the same as for PC stressors, as described earlier. Until this minimum data requirement has been established, comparison of the test-site median should be made with reference to the DGVs.
For those months, seasons or flow periods that constitute logical time intervals or events to consider and derive background data, the 80th percentile of background data (from a minimum of 10 observations) should be compared with the DGV. This 80th percentile value is used as the new guideline value for this period if it exceeds the DGVs. Compare test data with the new guideline values using the same principles outlined for PC stressors. Where background toxicant values fall consistently below DGVs, sampling intensity at these sites could be reduced after a suitable period (e.g. 2 years).
In practical terms, the method for comparing toxicant-test data with DGVs should be similar to the approach recommended for PC stressors. However, we recommend you apply a more conservative approach to the comparison of toxicant monitoring data with DGVs. Specifically, we recommend that a toxicant DGV is deemed to be exceeded if the 95th percentile of the test distribution exceeds the DGV (or stated differently, there has been no exceedance of the DGV if 95% of the values fall below the DGV). Additional guidance on this is provided in Toxicant default guideline values for water quality in aquatic ecosystems.
We recommend the more stringent approach here because, unlike PC stressors, toxicant DGVs are based on actual biological-effects data and so, by implication, exceedance of the DGV indicates the potential for ecological harm. Because the proportion of values required to be less than the DGV is very high (95%), a single observation greater than the DGV would be legitimate grounds for determining that an exceedance has occurred in most cases, even early in a sampling program.
In many situations, particularly where additional human use activities are present ‘upstream’ of the test site, the regular collection of data from upstream of the test site will be necessary. These data will be compared with the test data of interest to assist in determining the source and cause of any possible elevated toxicant concentrations found at the test site.
Where there are multiple sources of toxicants along a waterway, you will need to establish and apply appropriate data analysis and assessment procedures.
Sediments
As with toxicants in surface waters, guideline values for toxicants in sediments may be derived from reference or background site concentrations if these exceed the DGVs.
The selection of an acceptable reference site for toxicants in surface waters was discussed earlier. Basically the same considerations apply to sediments, with the additional option that a reference or background condition can also be established from measurements at depths in sediment cores below observed concentration excursions.
While temporal variability is used to characterise water quality parameters at a reference site, this is clearly inappropriate for sediments where the accumulation rates are typically below 1 cm/year. It is more appropriate to characterise a site using spatial variability, either based on depth profiles at a test site or an appropriate number of surface sediment samples.
Sites will typically contain a range of grain sizes, and determining median concentrations and 80th or 95th percentile values may distort any comparison. It is important to use samples with a similar grain-size distribution when comparing test and reference sites. Normalising to a fine grain size (e.g. < 63 μm) is inappropriate because the normalised value will have less of an impact on biota when diluted with coarser sediments that usually contain lower contaminant concentrations.
The spatial scale over which the reference-site and test-site measurements are taken is a matter for decision by stakeholders, based on sound scientific judgement.
The heterogeneity of sediment samples with respect to contaminants largely mirrors the differences in grain size.
Defining the size of the test site will be a regulatory responsibility, in terms of the spatial extent of contaminated sediment that is acceptable in the region of interest. As a guide, the spatial extent of a test site may:
- be a geographical feature (e.g. a delta or an embayment in a harbour)
- comprise a recognised ecological habitat (e.g. a riffle zone in a stream or a defined area of fine sediment in a lake).
In a large water body, the test site might be larger than a narrow river or creek and biota might have difficulty in avoiding the contamination.
The area of any reference site should be comparable to that of the test site and the grain size of the sediment at each site must be similar.
Because of the poor reliability of the sediment DGVs, it is difficult to be prescriptive about how these can be compared with test values. The same applies to the comparison of reference-site values with test sites, where comparisons of the reference median or 80th percentile with the test-site median may be equally appropriate in giving an estimate of the relative concentrations, which is really all that is required in the case of sediments.
Where sediment samples within a test site clearly exceed guideline values, or are reasonably inferred to be ecologically hazardous, the Water Quality Guidelines recommend additional sampling to more precisely delineate contaminated zones within the site.
Deriving guideline values in different government jurisdictions
Physical and chemical guideline values derived for moderately disturbed waters — the Queensland approach
In Queensland, water quality guideline values are a key input to water quality objectives listed in Schedule 1 of the Environmental Protection (Water and Wetland Biodiversity) Policy 2019. The policy seeks to achieve the objective of the Environmental Protection Act 1994, to protect Queensland waters while allowing for ecologically sustainable development.
The Queensland Government seeks to establish appropriate water quality objectives for all Queensland waters and prefers to use guidelines developed from local data to set those objectives.
The method outlined here shows how local water quality data are used to develop guideline values in moderately disturbed catchments.
Levels of protection
The Water Quality Guidelines define 3 levels of protection for aquatic ecosystems. At the state level, Queensland has expanded this to 4 levels of protection by splitting ‘slightly to moderately disturbed’ into ‘slightly disturbed’ and ‘moderately disturbed’ (Table 2).
| Water Quality Guidelines | Queensland Government | Description from Environmental Protection (Water and Wetland Biodiversity) Policy 2019 (Qld) |
|---|---|---|
| High conservation or ecological value | High ecological value (HEV) | Waters in which the biological integrity of the water is effectively unmodified or highly valued |
| Slightly to moderately disturbed | Slightly disturbed (SD) | Waters that have the biological integrity of high ecological value waters but with slightly modified physical or chemical quality |
| Moderately disturbed (MD) | Waters in which the biological integrity of the water is adversely affected by human activity to a relatively small but measurable degree | |
| Highly disturbed | Highly disturbed (HD) | Waters that are significantly degraded by human activity and have lower ecological value than slightly or moderately disturbed waters |
Creation of the moderately disturbed category is a recognition that large areas of Queensland catchments are extensively cleared and riparian areas greatly diminished. It is unlikely that these streams will ever return to an undisturbed condition so expectations of improvements in their condition need to be realistic and achievable.
This example describes an approach for developing guideline values for moderately disturbed waters that is aimed at realistic and attainable improvement in their condition.
Scope of guideline indicators
Water quality guideline values for aquatic ecosystem protection are clearly aimed at protecting the biota resident in, and directly associated with, waterways. Water quality guideline values have traditionally focused on PC stressors but in many streams, issues of habitat condition and stream flows are arguably as important as, or more important than, traditional water quality measures.
For this reason, in Queensland, the scope of ‘water quality guideline values’ has been expanded to include guideline values for habitat (e.g. riparian condition, stream barriers and presence of important refuge waterholes). Issues of environmental flows are generally handled under a separate water resource planning process, which sets analogous guideline values for a range of flow indicators.
Indicators of biota condition are also a key component of water quality guideline values. They provide an assessment of stream condition that integrates the effects of water chemistry, habitat and stream flows and thus indicate whether the overall stream management regime has successfully protected the biota. Wherever data are available, Queensland water quality guideline values include biological indicators.
For the purposes of this description, however, the focus is on approaches to developing suitable referentially based guideline values for PC stressors. Toxicant indicators are not in this scope; Queensland jurisdictions would normally default to the Water Quality Guidelines for these indicators.
Guideline methodology
As outlined as a general approach for aquatic ecosystems, ‘best available’ reference sites for modified ecosystems may provide the only choice for the reference condition. This is because truly undisturbed reference sites are sparse or absent, and even if available, they provide benchmarks that are unattainable within the foreseeable future.
Using this principle, guideline values for moderately disturbed waters in Queensland should be based on water quality at the least disturbed sites within the moderately disturbed region. These least disturbed sites thus become the reference condition for sites in modified ecosystem condition. The underlying aim is to bring all streams in the moderately disturbed region up to the quality of the less disturbed sites in that region, which is a potentially achievable aim.
Notwithstanding this, there is always an underlying principle that guideline values should continue to protect and improve the integrity of ecosystem function and general biological health.
Steps in the Queensland process:
- Define the region for which guideline values are to be developed. In Queensland, this would normally be a single large catchment or a basin containing a number of smaller catchments.
- Identify the moderately disturbed catchment areas in the region. There is no precise definition of ‘moderately disturbed’ but it would generally include catchments where there is extensive land clearing and loss of riparian vegetation.
- As required, subdivide the moderately disturbed catchments into homogenous groups or subregions based on geomorphology or water quality characteristics, or both. The extent to which it is practical to undertake this subdivision will often be constrained by the availability of monitoring sites or data. Where a number of similar catchments are involved, the regionalisation may simply comprise 2 categories across all catchments: upland and lowland. Very large catchments might be subdivided into their component subcatchments.
- Compile all available water quality data from each of the defined subregions.
- Stratify flow data. In theory, this could be based on a continuous flow versus water quality data relationship (e.g. flow vs electrical conductivity). However, there are rarely enough data to do this and, in practice, flow stratification is normally limited to sorting the data into high-flow and low-flow datasets. (Water quality data collected under high-flow conditions, when overland flow is occurring, is effectively a different population of values compared to data collected under other flow conditions so it should be treated separately.)
If flow data are available, the decision on where to place the high-flow/low-flow divide is based on an assessment of the flow duration curve and the water quality data. A common default is to define all data collected during the upper 10th percentile of flows as high-flow data but, based on more detailed assessment of the flow data, values ranging from 5 to 20% have been applied. If no flow data are available, rainfall can be used as a surrogate. The low-flow data are then used to create guideline values for application under low-flow conditions.
High-flow data can potentially be used to create separate high-flow guidance although this is often problematic due to data limitations and the high level of variation.
Low-flow guidance
- Assess the datasets in each region or subregion to help identify better quality sites. This is a key step. In effect, the better quality sites become the reference sites for that particular region or subregion. The sorting process can be based on the extent of site disturbance (e.g. catchment clearing, land use, riparian condition) or existing water quality, or both.
- Use the data from the identified set of regional or subregional reference sites to derive guideline percentiles. As these reference sites are to some extent already affected, the intent is to improve water quality. Therefore the guideline values are based principally on the 40th percentile (for stressors that cause problems at high concentrations) or 60th percentile (for stressors that cause problems at low levels), or both. For assessment including compliance, these values are compared against 50th percentile values at test sites, which provides some improvement in water quality.
- Review the guideline values derived through this process with respect to possible biological and downstream effects. You should aim to ensure that the guideline values support all but the most sensitive biota that occur naturally in these streams. There is also a need to consider downstream ecosystems. A particular example in Queensland is the need to manage nutrient levels in streams discharging to the Great Barrier Reef lagoon. Based on such considerations, some adjustment to the guideline values may be required.
- Apply the guideline values with caution under nil-flow conditions, particularly when there has been no flow for some time.
High-flow guidance
Derivation of high flow guideline values is much more problematic due to the high variability of water quality under high flows.
Guideline values can potentially be set in terms of:
- loads per unit of rainfall, or
- event mean or maximum concentrations.
The actual guideline values can be set as defined reductions in the loads or concentrations at the monitoring point (e.g. a 10% reduction).
For Great Barrier Reef catchments, guideline values have been set in terms of load reductions aimed at achieving specific improvements in the quality of reef waters. The specified load reductions are based on modelling of the effects of catchment loads on reef lagoon water quality and then using the model to predict the reduction in loads required to achieve the reef water quality guideline values.
Assessing statistically valid compliance with load guideline values presents considerable difficulties so there is necessarily a strong reliance placed on model predictions of the effect of changes in management practices on catchment loads.
Water quality objectives set for modified ecosystem conditions — the Victorian approach
Objectives in policies set to protect ecological health often indirectly set water quality objectives for poorer quality streams. A criticism often directed at such objectives in Victoria is that they are too far out of reach and considered ‘aspirational’, consequently resulting in little action to address problems.
In the review of Victoria’s overarching water quality policy, it has been proposed that providing objectives between current and desired condition may facilitate greater action. Alternative objectives in policy that recognise a greater degree of modification could be used as interim water quality objectives in management plans.
The Victoria Government has developed water quality objectives for 3 tiers of ecosystem condition (Table 3).
| Water Quality Guidelines | Victorian Government | Generic description of level of protection |
|---|---|---|
| High conservation or ecological value | Near natural (aquatic reserves) | Undisturbed |
| Slightly to moderately disturbed | Tier 1 (largely unmodified) | Ecologically healthy |
| Tier 2 (slightly to moderately modified) | Moderately disturbed | |
| Highly disturbed | Tier 3 (highly modified) | Highly disturbed |
No change to background is allowed in aquatic reserves so no specific objectives were proposed for that category. There is an inevitable subjectivity in assigning these categories to streams and multiple narrative statements have been developed to help support this, for example:
- Tier 1 — ‘catchment not heavily impacted but some change from a near natural state has occurred’
- Tier 2 — ‘many important natural features and functions are still present but will often require ongoing management for them to persist’
- Tier 3 — ‘most community values are lost or are at risk of being compromised’.
The reference condition approach still underpins this process, and a specialised geographic information system (GIS) called the Australian Hydrological Geospatial Fabric (Geofabric) is used to identify reference sites in the different tiers.
Within a buffer area of 1 km from each side of the stream and for 20 km upstream of the monitoring site, 5 metrics from the Geofabric measure:
- proportions of tree cover, intensive agriculture, sealed roads (surrogate for urban density) and mining
- flow disturbance index.
All metrics are range standardised to be between 0 and 1.
In Victoria, the state was previously classified into regions with water quality objectives set specifically in a region. Although the regions were classified based on macroinvertebrate community structure, they also reflected natural gradients in climate and topography. For regions with sites and catchments that were in near-natural or largely unmodified condition, the standard national approach of using data from good quality reference sites can be used to set objectives.
As all sites are rated by the same metrics from the Geofabric, the next best set of sites in a region were identified to become Tier 2 reference sites. These were sites with poorer quality streamside vegetation, more intensive agriculture and more roads than the reference sites used for Tier 1, but not the worst sites in the segment based on those metrics.
Potential Tier 2 or Tier 3 candidate reference streams were also assessed where possible with macroinvertebrate information from sites at or nearby them. This enabled an independent perspective to be gained as to the condition of the sites. The biological scores from candidate reference streams in Tier 2 were in what would be considered as moderate-to-good condition. (SIGNAL1 scores were mid-5s or above, there were generally 10 or more Ephemeroptera, Plecoptera and Trichoptera [EPT] families, and AUSRIVAS scores were generally greater than 0.8.)
As a further check, water quality at these tiered reference sites was checked for anomalies and sites were discarded on that basis. Discarding sites in this way reflects cause-and-effect understanding and the limitations of broadscale catchment condition information.
Data from the final set of tiered reference sites was then used to derive guideline percentiles for that tier, using the 75th percentile — the standard approach in Victoria.
Deriving and testing flow-based guideline values
It is not uncommon for the water quality to change in response to temporal factors, such as season or time of year. When there are fairly systematic changes to the expected condition in response to such factors, it may make sense to derive guideline values that take those factors into account.
Flow is often a key driver of water quality.
Consider the following example from Limestone Creek in the Kimberley region of northern Western Australia and to which the Argyle diamond mine discharges salts (MgSO4) (Van Dam et al. 2014).
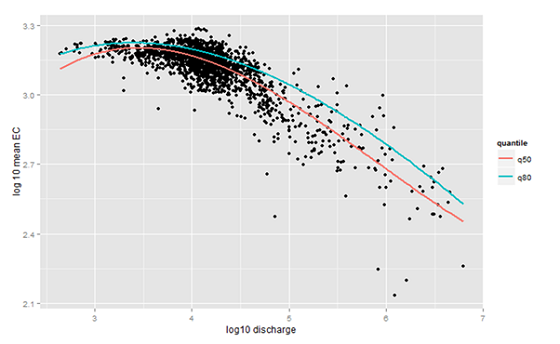
The strong relationship between (log) receiving stream discharge and (log) electrical conductivity (EC) in Figure 4 reflects seasonal differences and dilution. The data represented in this relationship are strongly mine-influenced. However, and for the purposes of this demonstration, the data could also represent natural relationships commonly found in the absence of human disturbance. If the relationship was ignored and only the log EC data were considered, 3.15 and 3.19 would be the values for the 50th and 80th percentiles, respectively. From Figure 4, these are clearly much higher than the log EC that would be expected under higher discharge conditions, and most likely due to the dilution.
An alternative is to derive guideline values that change with the discharge. This might be achieved by creating several categories for discharge and estimating the percentiles for each. In Figure 4, this has been done continuously using quantile regression with a spline relationship between log EC and log discharge to represent the non-linear nature of the relationship. The 2 lines on Figure 4 are the estimated flow-dependent 50th percentile (or quantile) and 80th percentile (or quantile), respectively.
Incorporating more flexible guideline values, such as those presented in Figure 4, can increase the power to detect changes. It also helps avoid situations and wasted effort where the application of standard guideline values are only ever likely to be exceeded at certain times of the year or under specific conditions.
The representation in Figure 4 is clearly descriptive. The key recommendations here are to:
- think carefully about the situations under which the guideline values make sense
- explore whether there is structure to the expected water quality under reference conditions that should be incorporated.
This may also point to how that water body may be managed. In this particular example, if the water body was receiving a discharge at the time of the high flow, notionally more salinity or EC could be added without necessarily causing adverse effects to the receiving ecosystem.
Alternatively, if the data represented an undisturbed ecosystem with natural flow-related change in water quality, a management goal could include a desire to maintain similar water quality across the hydrograph (high EC at low flow, low EC at high flow).
Extending this example further, it is possible to consider how changes might be assessed with flow-based guideline values. For instance, if an additional n observations were taken subsequently (or at an additional comparable site) and x of those exceeded the flow-dependent guideline value for the 80th percentile, across all flow values, do you think that there has been a change? If 33% of the n observations exceed their appropriate 80th percentile (rather than the expected 20%), has there been a shift? While on the face of it the answer may seem obvious given that 33% clearly exceeds the expected 20%, the answer is that it depends. If the sample size n for estimating the proportion that exceed is small, then that estimate of the proportion exceeding is not well estimated.
For example, if n = 12 and 4 out of the 12 (33%) samples exceed their flow threshold, then the probability of at least 4 exceedances, assuming the conditions represented in Figure 4 are met, is obtained from a binomial distribution with n = 12 and p = 0.2 and is given by:
Prob(X ≥ 4) = 0.205
Table 4 shows the probability of at least one-third of the observations exceeding the flow-dependent guideline values by chance for different sample sizes. As the sample size increases, it is possible to be much more definitive about the likely change to water quality.
| Sample size n | Observed number exceeding (33%) | Probability of 33% or more exceeding flow-dependent guideline values given sample size n and p = 0.2 |
|---|---|---|
| 12 | 4 | 0.205 |
| 24 | 8 | 0.089 |
| 36 | 12 | 0.042 |
| 48 | 16 | 0.021 |
This example causes us to question the magnitude of the change that it is important for a water quality monitoring program to be able to detect that change. Moreover, it illustrates a situation where the burden of proof should be considered explicitly.
A null hypothesis of no change requires the monitoring program to provide enough evidence to detect and support the alternative hypothesis of change (or non-compliance). As discussed earlier, the decision on what to assume as the null hypothesis is an important one and needs to balance the risks and costs of the respective errors.
Next steps:
References
Barnett V & O’Hagan T 1997, Setting Environmental Standards: The statistical approach to handling uncertainty and variation, Chapman and Hall, London.
Chakraborti S & Li J 2007, Confidence interval estimates of a normal percentile, The American Statistician 61: 331–336.
Cochran WG 1977, Sampling Techniques, 3rd Edition, Wiley, New York.
Esterby S 1989, Some statistical considerations in the assessment of compliance, Environmental Monitoring and Assessment 12: 103–112.
Fairweather PG 1991, Statistical power and design requirements for environmental monitoring, Australian Journal of Marine and Freshwater Research 42: 555–567.
Gibbons RD 2003, A statistical approach for performing water quality impairment assessments, Journal of the American Water Resources Association 39(4): 841–849.
Goudey R 2007, Do statistical inferences allowing three alternative decisions give better feedback for environmentally precautionary decision-making? Journal of Environmental Management 85: 338–344.
Hyndman RJ & Fan Y 1996, Sample quantiles in statistical packages, The American Statistician 50: 361–365.
Mac Nally R & Hart BT 1997, Use of CUSUM methods for water-quality monitoring in storages, Environmental Science & Technology 31: 2114–2119.
McBride GB 2003, Confidence of compliance: parametric approaches versus nonparametric approaches, Water Research 37: 3666–3671.
McBride GB 2005, Using Statistical Methods for Water Quality Management: Issues, options and solutions, Wiley, New York.
McBride GB & Ellis JC 2001, Confidence of compliance: a bayesian approach for percentile standards, Water Research 35: 1117–1124.
MfE 2003, Microbiological Water Quality Guidelines for Marine and Freshwater Recreational Areas, ME 474, New Zealand Ministry for the Environment, Wellington.
Särndal CE, Swensson B & Wretman J 1992, Model-assisted survey sampling, Springer-Verlag, New York.
Schoonjans F, De Bacquer D & Schmid P 2011, Estimation of population percentiles, Epidemiology 22: 750–751.
Shabman L & Smith EP 2003, Implications of applying statistically based procedures for water quality assessment, Journal of Water Resources Planning and Management 129(4): 330–336.
Smith EP, Ye K, Hughes C & Shabman L 2001, Statistical assessment of violations of water quality standards under Section 303(d) of the Clean Water Act, Environmental Science & Technology 35: 606–612.
Smith EP, Zahran A, Mahmoud M & Ye K 2003, Evaluation of water quality using acceptance sampling by variables, Environmetrics 14: 373–386.
van Dam RA, Humphrey CL, Harford AJ, Sinclair A, Jones DR, Davies S & Storey AW 2014, Site-specific water quality guidelines: 1. Derivation approaches based on physiochemical, ecotoxicological and ecological data, Environmental Science and Pollution Research 21: 118–130.
Walshe T, Wintle B, Filder F & Burgam M 2007, Use of confidence intervals to demonstrate performance against forest management standards, Forest Ecology and Management 247: 237–245.