Modelling approaches for monitoring data
Before reading this page, you should read:
Most statistical analyses are concerned with inference (the methods we use to infer something about some characteristic of a population of values) based on the limited information contained in a sample drawn from that population.
Here we briefly explain different modelling philosophies used when analysing data in water quality monitoring programs. The distinction between model-based and probability-based analyses is outlined and followed by a discussion on Bayesian and frequentist methods. Then we explain Bayesian inference concepts and how they link to hierarchical models and expert opinion.
Model-based versus probability-based analysis
When it comes to spatial monitoring design, 2 popular statistical philosophies for choosing a sampling strategy are:
Other statistically valid methods for choosing sample sites that exist in broader environmental or ecological contexts may be relevant for sampling aquatic resources, including geometric approaches (e.g. Muller 2000) and hybrid approaches (e.g. Cressie et al. 2009, Brus & De Gruijter 2012).
With regard to analysis of water quality data, choosing an appropriate approach will primarily be determined by the objectives of the study. The adopted sampling strategy can also help guide analysis options.
If a model-based design is used to select sample sites, then the ensuing data can only be analysed using a model-based approach.
If probability-based designs are used for site selection, then the data can be analysed using readily available survey sample methods or a statistical model.
Probability-based analysis
Probability-based designs enable inference about an attribute of the population, such as a mean, total, variance, proportion or distribution function to extend from the observed sample to the population.
For example, repeated random subsampling from a grab sample yields data that could be used to determine average levels of a water quality indicator of interest for that sample. Sampling at sites on a stream network will yield data that can be used to determine the length of the network that is of a particular condition.
The central feature is that representativeness of the population can follow naturally from probability-based sampling if designed carefully. Inferences more often follow directly from simple statistics.
Model-based analysis
Model-based analyses rely heavily on the form of the model, its ability to capture the potential complexity in the system of interest and its generality for making valid, reliable and precise predictions and inferences.
Model-based inference can be very general and precise from a limited number of sample observations.
Reliability of the inference, on the downside, depends on:
- conceptualisation of the underlying processes or system (identified at Step 1 of the Water Quality Management Framework)
- adequacy of their representation in the model formulation
- availability of sufficient data.
Discussion about the contrasts between the 2 approaches is well documented in the literature. Refer to Sarndal (1978) and Hanson et al. (1983) for general discussion. De Gruijter & Ter Braak (1990) and Brus & De Gruijter (1993, 1997) focused on the differences in spatial inference in the context of soil sampling, and Theobald et al. (2007) outlined the differences in relation to environmental monitoring of natural resources generally.
Here we focus on model-based analyses because they are appropriate for either probability-based or model-based study designs.
Bayesian versus frequentist approaches
Bayesian methods have taken a prominent role in modelling complex environmental processes in recent times (Kang & Cressie 2013, Parslow et al. 2013, Berrocal et al. 2014, Clifford et al. 2014, Pagendam et al. 2014, Zammit-Mangion et al. 2014). Their flexible nature, inherent in the hierarchical set up, provides an attractive framework for modelling that can accommodate information sources at different spatial and temporal scales. The incorporation of expert opinion when other quantitative information is lacking can assist with prediction and assessment that may have otherwise been abandoned.
Compared with frequentist approaches, Bayesian methods offer flexibility for modelling, estimation and assessment but at the expense of the additional computational capability required for implementation.
Frequentist approaches are philosophically distinct from Bayesian methods in many — sometimes subtle — ways. This is why one approach may be chosen over another when defining a framework for modelling.
As Casella (2008) pointed out, frequentists house an orthodox view to statistical inference whereby ‘sampling is regarded as infinite and decisions are sharp’. This infers that the data arise from a repeatable sample where the underlying parameters are constant and remain fixed.
Bayesians consider unknown quantities as random variables with assigned probability distributions that can be updated when new information becomes available. Under this statistical philosophy, the data are considered fixed (Gelman et al. 2004). The notion of confidence or credible intervals can be considered a subtle interpretation despite having quite different interpretations.
The interpretation of a frequentist 95% confidence interval, for example, is one that results from repeating an experiment an infinite number of times, and from this, estimating the quantity of interest (e.g. mean), resulting in 95% of the estimated means lying within the confidence interval.
A 95% Bayesian credible interval can be interpreted as having a 95% probability that the mean lies within the credible interval, given the data.
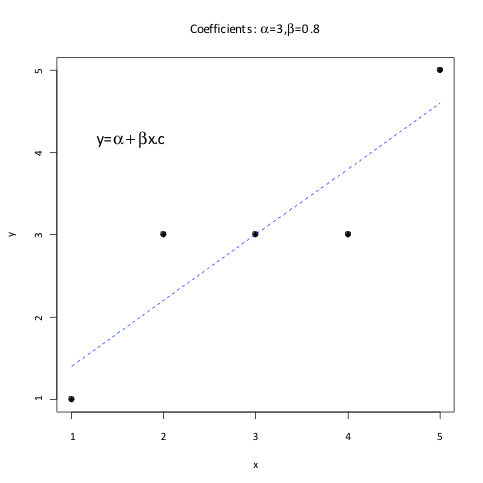
We can perform an analysis on a very simple dataset to contrast the 2 approaches, which has been presented many times as the ‘line example’ in the literature.
The line example consists of 5 pairs of points, {x,y} = {(1,1), (2,3), (3,3), (4,3), (5,5)} that roughly lie along a straight line, as illustrated in Figure 1.
The model formulation in this simple case assumes:
Y ~ N(α + β(x – x̅),1/τ2).
This can be easily fit in a frequentist framework using the method of least squares but we also performed a Bayesian analysis and contrasted the results in Table 5 . The parameter estimates produced for both analyses are very similar for this example but not exactly the same. The confidence interval for τ, which is the square root of the precision parameter (square root of the reciprocal of the residual variance) is not provided for the least squares estimate because it is not routinely provided as part of the model output.
| Parameter | α | β | τ | |
|---|---|---|---|---|
| Bayesian | Estimate | 3.001 | 0.800 | 1.894 |
| Standard deviation | 0.55 | 0.38 | 1.53 | |
| 95% credible interval | [2.00,4.07] | [0.09,1.53] | [0.14,5.89] | |
| Least squares | Estimate | 3.000 | 0.800 | 1.875 |
| Standard deviation | 0.33 | 0.23 | – | |
| 95% credible interval | [1.95,4.05] | [0.07,1.53] | – | |
Within the context of the Water Quality Management Framework, while Bayesian and frequentist approaches to the analysis and the incorporation of updates or existing knowledge may differ, the overarching focus needs to be on the quality of the inferences and the level of support for the underlying assumptions.
Ask yourself, ‘What inferences do the analyses enable us to make that are relevant to the water quality objectives?’
Bayesian inference, hierarchical modelling and expert opinion
We outline the general concepts of Bayesian inference because it has taken a prominent role in the analysis of environmental and ecological data (Kuhnert et al. 2005, Martin et al. 2005, Griffiths et al. 2007, Fox 2010, Pagendam et al. 2014). You can read more comprehensive references on the topic (Robert 2001, Gelman et al. 2004).
Let θ represent a vector of unobservable quantities, y the observed data and x a vector of explanatory variables. If we consider the joint distribution of θ and y such that:
p(ϑ,y) = p(ϑ)p(y|ϑ)
where p(ϑ,y) represents the joint distribution of θ and y, p(ϑ) represents prior probability distributions and our initial belief for θ, and p(y|ϑ) represents the sampling distribution (also known as ‘data distribution’ or likelihood that characterises the data). If the data, y, is taken as known or fixed (conditioned on), the posterior distribution p(ϑ|y) is obtained through Bayes theorem and is expressed in Equation 1.
Equation 1
The posterior distribution is of central importance in Bayesian analysis because it summarises the state of knowledge by combining the prior information with information gained through the observed data. The posterior distribution can be used to provide point estimates, interval estimates or other summary features.
Often the denominator in Equation 1 is difficult to evaluate in closed form with the exception of simple problems. It is easier, although more computationally complex, to simplify the expression in Equation 1 and work with an un-normalised density as shown in Equation 2. Simulation methods using Markov chain Monte Carlo (MCMC) can then be used to approximate the denominator.
Equation 2
p(ϑ|y) µ p(ϑ)p(y|ϑ)
Probably the most popular of the MCMC algorithms is Gibbs sampling. The Metropolis and Metropolis–Hastings algorithms (Casella & Robert 2004) work reasonably well for simple models.
As problems have become more complex and hierarchical in nature, other algorithms have been considered to assist with convergence and optimisation issues (Doucet et al. 2001, Andrieu et al. 2010). These types of problems generally have greater computational requirements and may need high performance computing support, in addition to smart and efficient ways of implementing them (Murray 2013). This is outside the scope of the Water Quality Guidelines but you can read the publications cited for important discussion on this topic.
Hierarchical modelling and the concept of conditioning give Bayesian analysis the flexibility to accommodate different sources of information and uncertainty at different spatial and temporal resolutions (Cressie et al. 2009). In environmental applications, observations are typically measured across space and through time and there is a need to characterise the underlying processes.
Hierarchical models exist in the frequentist paradigm through multi-level modelling or mixed-effects modelling (e.g. Bates 2010, Pinheiro & Bates 2000) but they may be more easily accommodated in a Bayesian framework, particularly where it is important to estimate the uncertainty at all hierarchical layers of modelling.
As we highlighted earlier, and in Cressie et al. (2009), the key to hierarchical modelling is conditional thinking: observing A conditional on B and B conditional on C and so on. Cressie et al. (2009) outlined some ecological examples in relation to this.
Physical-statistical modelling has focused on the assimilation of measurements with models of underlying processes in an attempt to capture all aspects of a complex system (Kuhnert 2014).
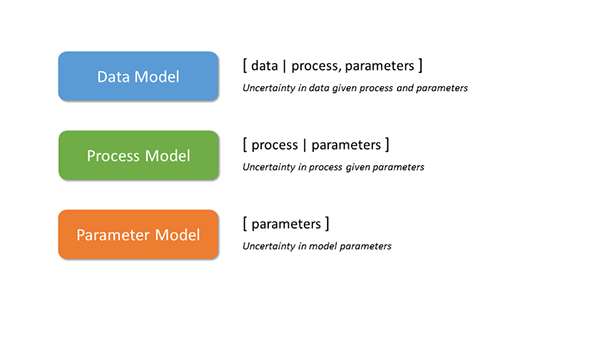
The statistical framework housing this concept is a Bayesian hierarchical model (BHM), as expressed in Equation 3 and outlined in Cressie & Wikle (2011) and Berliner (1996).
Equation 3
[Z,Y,ϑ,s] = [Z|Y,s] x [Y|ϑ] x [ϑ,s]
where
[Z|Y,s] = data model
[Y|ϑ] = process model
[ϑ,s] = prior parameters model
and Z represents data on some process Y with process model parameters θ and statistical parameters s, and [] represents some probability distribution appropriate for the data.
Alternatively, this representation could be viewed through the diagram in Figure 2, which highlights the uncertainty we wish to accommodate at each hierarchical layer of the model.
Examples of this type of approach being applied to environmental problems are outlined in the special issue on physical-statistical modelling (Kuhnert 2014) and included the work of Berrocal et al. (2014), Clifford et al. (2014), Pagendam et al. (2014) and Zammit-Mangion et al. (2014).
One of the key outputs from this type of modelling paradigm is the ability to clearly and transparently capture all sources of uncertainty.
Being able to capture and incorporate this information into a BHM allows the quantification of the uncertainty or realisation of the level of confidence in the predictions. This can be formulated in a risk-based framework, similar to the work of Hayes et al. (2011) and Berrocal et al. (2014) to assess the probability of exceeding a specified guideline value or threshold.
This type of modelling can be extremely important when setting new guideline values for a monitoring program, particularly if the existing ones were based on limited information or were qualitatively defined.
The role of expert opinion in BHMs is important, particularly if the model is relying on additional well-informed data to assist in the quantification of one or more parameters from the model. Burgman (2005), Low-Choy et al. (2009) and Kuhnert et al. (2010) outlined the role of expert opinion in ecological models and presented useful guides on the elicitation process to avoid any potential biases.
Expert information enters into a BHM through a prior probability distribution (known as the ‘prior’) that captures the expert’s belief about the parameter of interest. If the prior is quite tight and hence informative, it represents the confidence conveyed by the expert around their response. If the prior is reasonably vague or uninformative, it represents the expert’s lack of knowledge about the subject of interest.
Several publications focus on expert judgement and the biases inherent in eliciting information from experts (O'Hagan et al. 2006, Carey & Burgman 2008, Low-Choy et al. 2009, Kuhnert et al. 2010, Burgman et al. 2011, McBride et al. 2012). Several tools make the elicitation process easy to implement (O'Hagan & Oakley 2008, Speirs-Bridge et al. 2009, Low-Choy et al. 2011).
In many BHMs, uninformative (but proper) priors are placed on parameters, such as variances and regression coefficients, when there is little or no information available to inform them. In these instances, the algorithms used to evaluate the models will estimate the parameters and quantify the uncertainty for each.
Bayesian belief networks (BBNs) have become popular in environmental and ecological domains because they offer an approach that is palatable to managers and stakeholders and allow for complex statistical conversations to occur.
The underlying model supporting the BBN is Bayes theorem (Equation 2), with inputs into the model being expressed through conditional probabilities. Several popular software can implement BBNs.
Criticisms around the development and structure of BBNs include:
- the lack of any feedback loops and the processes (discretisation, scaling, structure and complexity) that are used to develop them (Kuhnert & Hayes 2009)
- that a BBN without the development of the posterior distributions will suffer from the quality of the priors, particularly where those are uninformative or vague because of information gaps.
Despite this, many BBNs have been used to help structure conversations around environmental problems and assist in decision-making, risk assessments through weight-of-evidence approaches, and guideline value setting initiatives (Hamilton et al. 2007, Johnstone et al. 2009, Ayre et al. 2014).
Next steps:
References
Andrieu C, Doucet A & Holenstein R 2010, Particle Markov chain Monte Carlo methods, Journal of the Royal Statistical Society, Series B: Statistical Methodology 72: 269–342.
Ayre KK, Caldwell CA, Stinson J & Landis WG 2014, Analysis of regional scale risk of whirling disease in populations of Colorado and Rio Grande cutthroat trout using a Bayesian belief network model, Risk Analysis 34: 1589–1605.
Bates DM 2010, lme4: Mixed-effects Modeling with R, Springer, New York.
Berliner LM 1996, Hierarchical Bayesian time series models, in: Hanson KM & Silver RN (eds), Maximum Entropy and Bayesian Methods, Springer, Netherlands.
Berrocal VJ, Belfand AE & Holland DM 2014, Assessing exceedance of ozone standards: a space-time downscaler for fourth highest ozone concentrations, Environmetrics 25: 279–291.
Brus DJ & De Gruijter JJ 1993, Design-based versus model-based estimates of spatial means: Theory and application in environmental soil science, Environmetrics 4: 123–152.
Brus DJ & De Gruijter JJ 1997, Random sampling or geostatistical modeling? Choosing between design-based and model-based sampling strategies for soil (with discussion), Geoderma 60: 1–44.
Brus DJ & De Gruijter JJ 2012, A hybrid design-based and model-based sampling approach to estimate the temporal trend of spatial means, Geoderma 173–174: 241–248.
Burgman M 2005, Risks and Decisions for Conservation and Environmental Management, Cambridge University Press, Cambridge.
Burgman M, Carr A, Godden L, Gregory R, McBride M, Flander L & Maguire L 2011, Redefining expertise and improving ecological judgment, Conservation Letters 4: 81–87.
Carey J & Burgman M 2008, Linguistic uncertainty in qualitative risk analysis and how to minimize it, Annals of the New York Academy of Sciences 1128: 13–17.
Casella G 2008, Bayesians and Frequentists: Models, assumptions and inference (PDF, 1.2MB), Refresher on Bayesian and Frequentist Concepts presentation, Department of Statistics, University of Florida.
Casella G & Robert CP 2004, Monte Carlo Statistical Methods, 2nd Edition, Springer-Verlag, Berlin.
Clifford D, Pagendam DE, Baldock J, Cressie N, Farquharson R, Farrell M, Macdonald L & Murray L 2014, Rethinking soil carbon modelling: a stochastic approach to quantify uncertainties, Environmetrics 25: 265–278.
Cressie N, Calder CA, Clark JS, Ver Hoef JM & Wikle CK 2009, Accounting for uncertainty in ecological analysis: the strengths and limitations of hierarchical statistical modeling, Ecological Applications 19: 553–570.
Cressie N & Wikle CK 2011, Statistics for Spatio-Temporal Data, Wiley, New Jersey.
de Gruijter JJ & Ter Braak CJF 1990, Model free estimation from survey samples: A reappraisal of classical sampling theory, Mathematical Geology 22: 407–415.
Doucet A, De Freitas N & Gordon N 2001, Sequential Monte Carlo Methods in Practice, Springer, New York.
Fox D 2010, A Bayesian approach for determining the no effect concentration and the hazardous concentration in ecotoxicology, Ecotoxicology and Environmental Safety 73: 123–131.
Gelman A, Carlin JB, Stern H S & Rubin DB 2004, Bayesian Data Analysis, Third Edition, Chapman and Hall/CRC, New York.
Griffiths SP, Kuhnert PM, Venables WN & Blaber SJM 2007, Estimating abundance of pelagic fishes using gillnet catch data in data-limited fisheries: a Bayesian approach, Canadian Journal of Fisheries and Aquatic Science 64: 1019–1033.
Hamilton G, Fielding F, Chiffings AW, Hart BT, Johnstone RW & Mengersen K 2007, Investigating the use of a Bayesian network to model the risk of Lyngbya majuscula bloom initiation in Deception Bay, Queensland, Human and Ecological Risk Assessment 13: 1271–1279.
Hansen MH, Madow WG & Tepping BJ 1983, An evaluation of model dependent and probability sampling inferences in sample surveys, Journal of the American Statistical Association 78: 776–807.
Hayes K 2011, Uncertainty and uncertainty analysis methods, technical report, CSIRO Division of Mathematics, Informatics and Statistics, Hobart.
Johnstone S, Fielding F, Hamilton G & Mengersen K 2009, An integrated Bayesian network approach to bloom initiation, Marine Environmental Research 69: 27–37.
Kang EL & Cressie N 2013, Bayesian hierarchical ANOVA of regional climate-change projections from NARCCAP Phase II, International Journal of Applied Earth Observation and Geoinformation 22: 3–15.
Kuhnert PM 2014, Physical-statistical modelling, Environmetrics 25: 201–202.
Kuhnert PM & Hayes KR 2009, How believable is your BBN? (PDF, 350KB), in: Anderssen RS, Braddock RD & Newham LTH (eds), 18th World IMACS Congress and MODSIM09 International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand and International Association for Mathematics and Computers in Simulation: 4319–4325.
Kuhnert PM, Martin T, Mengersen K & Possingham HP 2005, Assessing the impacts of grazing levels on bird density in woodland habitat: A Bayesian approach using expert opinion, Environmetrics 16: 717–747.
Kuhnert PM, Martin T & Griffiths SP 2010, A guide to eliciting and using expert knowledge in Bayesian ecological models, Ecology Letters 13: 900–914.
Low-Choy S, O'Leary R, & Mengersen K 2009, Elicitation by design in ecology: using expert opinion to inform priors for Bayesian statistical models, Ecology 90(1): 265–277.
Low-Choy S, James A, Murray J & Mengersen K 2011, Elicitator: a user-friendly, interactive tool to support scenario-based elicitation of expert knowledge, in: Ajith H, Perera C, Drew A & Johnson CJ (eds), Expert knowledge and its application in landscape ecology, Springer, New York.
Martin T, Kuhnert PM, Mengersen K & Possingham HP 2005, The power of expert opinion in ecological models: a Bayesian approach examining the impact of livestock grazing on birds, Ecological Applications 15: 266–280.
McBride M, Fidler F & Burgman M 2012, Evaluating the accuracy and calibration of expert predictions under uncertainty: predicting the outcomes of ecological research, Diversity and Distributions 18: 782–794.
Muller WG 2000, Collecting Spatial Data: Optimum design of experiments for random fields, 2nd Edition, Physica Verlag, Heidelberg.
Murray LM 2013, Bayesian state-space modelling on high-performance hardware using LibBi, arXiv:1306.3277.
O'Hagan A, Buck CE, Daneshkhah A, Eiser JR, Garthwaite PH, Jenkinson DJ, Oakley JE & Rakow T 2006, Uncertain Judgements: Eliciting Experts' Probabilities, Wiley.
O'Hagan A & Oakley J 2008, SHELF: the Sheffield Elicitation Framework, School of Mathematics and Statistics, University of Sheffield.
Pagendam DE, Kuhnert PM, Leeds WB, Wikle CK, Bartley R & Peterson EE 2014, Assimilating catchment processes with monitoring data to estimate sediment loads to the Great Barrier Reef, Environmetrics 25: 214–229.
Parslow J, Cressie N, Campbell EP, Jones E & Murray LM 2013, Bayesian learning and predictability in a stochastic nonlinear dynamical model, Ecological Applications 23: 679–698.
Pinheiro JC & Bates DM 2000, Mixed-Effects Models in S and S-Plus, Springer, New York.
Robert CP 2001, The Bayesian Choice: From decision-theoretic motivations to computational implementation, Second Edition, Springer-Verlag, New York.
Sarndal C 1978, Design-based and model-based inference for survey sampling, Scandinavian Journal of Statistics 5: 27–52.
Speirs-Bridge A, Fidler F, McBride M, Flander L, Cumming G & Burgman M 2009, Reducing overconfidence in the interval judgments of experts, Risk Analysis 30(3): 512–523.
Theobald DM, Stevens DL Jr, White D, Urquhart NS, Olsen AR, & Norman JB 2007, Using GIS to generate spatially-balanced random survey designs for natural resource applications, Environmental Management 40: 134–146.
Zammit-Mangion A, Rougier J, Bamber J & Schon N 2014, Resolving the Antarctic contribution to sea-level rise: a hierarchical modelling framework, Environmetrics 25(4): 245–264.