Assessment of change through monitoring data analysis

Changes in water quality over time and space

Spatial or temporal components are often associated with data collection — especially in water quality monitoring studies. This is driven by the monitoring program objectives.

The larger the study region, the greater the chance that spatial dependence could occur at multiple spatial resolutions. Likewise, the longer the study, the greater the chance that temporal dependence may exhibit multiple temporal resolutions. These attributes are critical to be aware of, explore and factor into an analysis so you can make valid inferences.

Here we consider analysis options when a single water quality variable is measured at one site over time or at multiple sites for a particular point in time.

Spatial and temporal attributes of data are often non-separable so spatiotemporal analyses are more appropriate. In the case of multiple water quality variables measured, the appropriate analyses are even more complex, with a multivariate response being required (refer to Multivariate and high-dimensional data for a discussion of multivariate analyses).

Spatiotemporal modelling is an increasingly expanding area of statistical research with much traction due to the increased and varied spatial and temporal scales of data collection, particularly in the environmental domain. Discussion of these approaches is beyond the scope of the Water Quality Guidelines. Cressie & Wikle 2011 comprehensively covered approaches for analysis of spatiotemporal data.

The first step in an analysis of spatially or temporally referenced data is to establish if there is a trend. If there is a trend, then the challenge is to ascertain why there is a trend, quantify the specific nature of the trend, and ensure this relates back to the study objectives.

The choice of analysis approach or model complexity needs to suit the data density and attributes. Some methods may not be appropriate for small sample sizes or for high frequency data.

Using temporal analysis approaches

One of the principal objectives of water quality monitoring is to assess changes over time. In many instances, this is driven by the need to compare water quality against a guideline value, but there is also an important need to track changes over time in response to a management intervention or other drivers, such as land use, and identify potential trajectories or trends in water quality.

Here we consider approaches to the temporal analysis of water quality monitoring data under 3 subsections:

• water quality trend analysis
• time series analysis
• analysis of high frequency monitoring data.

The dependence of water quality drivers, such as flow and climate variability, appeal to related methods but are typically focused on understanding the drivers behind any of the temporal changes identified.

Water quality t​rend analysis

Although trend analysis is a popular tool in many fields, including environmental science, it is not a specific research topic in statistics. Instead, many statistical methods can be applied to extract an underlying pattern or behaviour by treating time as a variable. The exception is time series analysis, which was developed to deal with data collected over time (correlated data).

Formal statistical analysis of temporal data can be rather complex and requires a good degree of skill in identifying suitable models.

Numerous texts have been written on time series analysis: Chatfield (2003), Shumway & Stoffer (2006) and Brockwell & Davis (2016) provide good introductory-level information. Brillinger (1994), Esterby (1996) and Morton & Henderson (2008) reviewed different types of temporal trend and associated trend analyses.

It is highly recommended to explore the data series first using smoothing methods, such as LOWESS (locally weighted scatterplot smoothing) (Cleveland 1979) and kernel smoothing (Nadaraya 1964, Watson 1964), before adopting a particular method (see Data visualisation).

The objectives of a water quality trend analysis are often about trend detection or trend estimation.

The focus of trend detection is on determining whether or not there has been a departure from the background or historical conditions. This change is usually viewed as monotonic. Our interest is in establishing whether the condition is improving or deteriorating. Hypothesis testing may be used to determine if this change is statistically significant.

Trend estimation is distinct from trend detection in that the objective is to quantify the nature of the change and investigate models that provide the interpretation of the process possibly causing them. Trend estimation is typically of interest for longer periods of data and needs to allow the possibility of nonlinear trends.

Some of the difference between trend detection and estimation relates principally to the scale of interest, as summarised in Table 1.

Table 1 Focus of water quality trend analysis as a function of scale (Henderson & Morton 2008)

Scale	Short term (less than 1 year)	Medium term (3 to 8 years)	Long term (more than 8 years)
Focus	Detection of large rapid changes or anomalous events. Stronger alignment with data quality and QA/QC procedures.	Focus on trend detection. Typically the identification of monotonic changes. Are things improving, degrading or staying fairly constant?	Trend detection may still be important but greater emphasis on trend estimation. Nonlinear trends are likely in the longer term. How has the average value for a water quality parameter changed over time? Nature and shape of trend interpretable in its own right.
Methods	Outlier detection, Kalman filter, quality control charts, etc.	Seasonal Kendall’s tau, linear regression methods, robust regression, semi-parametric regression.	Linear and polynomial regression, robust regression, LOWESS, semi-parametric regression.

We briefly explain some statistical methods that can be used for analysis of temporal data.

Rank-based appro​aches

Rank-based (nonparametric) approaches are often used as trend analysis tools in water quality studies due to their distribution-free assumption, including Kendall’s tau (τ) test (Kendall 1938) and Spearman’s rho (ρ) test (Spearman 1904). Kendall’s τ test that accounts for seasonality is given in Gilbert (1987) and Helsel & Hirsch (1992). Both tests assume that the trends are monotonic (consistently increase or decrease). If concentrations vary non-monotonically over the period being analysed, the results of linear tests for trend may be misleading (Robson & Neal 1996). Furthermore, it is assumed that observations are independent. When applied to data series that are not independent (exhibit autocorrelation), the risk of falsely detecting a trend is increased (Ward et al. 1990, Esterby 1996).

As a general rule, the level of serial correlation in a data series increases as the frequency of sampling increases. The maximum sampling frequency possible without encountering serial correlation can be thought of as the ‘point of information saturation’ (Ward et al. 1990).

The seasonal Kendall test is based on:

where

S is then compared with a tabulated critical value to assess its significance. While the seasonal Kendall test is robust under a variety of conditions, it is nevertheless important to examine the data for outliers (refer to Censored data) and to adjust the data for the effect of nuisance variables.

For example, many water quality indicators are correlated with flow so the seasonal Kendall test should be applied to the residuals (flow-corrected observations). These residuals can be obtained either as data predicted, where predicted values are obtained by explicitly modelling the relationship between flow and the variable of interest (e.g. using a regression model), or by using a nonparametric smoother.

Linear regression

When there is certainty that the errors are normally distributed, regression methods are highly recommended because they easily handle different types of trend simultaneously and explain the trend using covariates.

Linear regression is the simplest form of regression with parameter estimates obtained using ordinary least squares (OLS). A straightforward extension is the polynomial regression, which consists of high-order terms in time that capture the nonlinear features in the trend. The seasonality can be captured by including the sine-cosine functions with different periods for different seasonality (e.g. year, month, week). To capture multiple changes over time, segmented regression can be performed.

Gallant & Fuller (1973) considered a case in which the regression function is continuous (regression segments joined together at the change point). Shao & Campbell (2002) generalised the segmented linear regression to include seasonality and different types of change points (either continuous or abrupt changes).

If the data demonstrate an abrupt change from one stable status to another stable status, then the Pettitt (1979) test may be useful.

Semi-parametric regression

Semi-parametric models refer to the fitting of arbitrary smooth curves in place of parametrically defined curves, such as lines or polynomials. The smooth curves are nonparametric in the true sense of the word. ‘Semi’ implies that some of the regression terms may be represented parametrically.

Smooth trend curves can be estimated by various methods, including splines, kernels and LOWESS, and under the broad generalised additive model (GAM) framework.

Spline trend models for water quality may be well represented by a GAM (Hastie & Tibshirani 1990, Wood 2006). This is a semi-parametric regression model where one or more of the additive terms take the form of an arbitrary smooth function. This function is nonparametric in that it does not follow a prescribed parametric formula. The property of smoothness enables its value at any point to be estimated from many observations locally in the regressor. A GAM necessarily tends to smooth over rapid changes, such as a sharp peak or trough or an abrupt change of level.

GAMs make the same assumptions as those used in ordinary regression and rely on independent residual errors that follow a normal distribution with constant variance. A lack of normality in the residuals does not invalidate the statistical inference but there is some loss of efficiency. Nonconstant variance does not bias the estimated regression parameters but it can give misleading standard errors, statistical significance and confidence intervals. This is not a serious issue unless the variance changes dramatically. The main concern is the non-independence of the errors. This is addressed by combining time series errors with the GAM. Equal spacing of the time points is not a requirement of a GAM any more than it is for an ordinary linear regression model. However, unequal spacing or missing data in any regression can create additional difficulties when time series errors are used.

Examples of semi-parametric water quality trend analysis include Miller & Hirst (1998), Schreider et al. (2002) and Morton & Henderson (2008).

Robust regression

In terms of parameter estimation and identification of a good-fitting model, a significant drawback of the ‘conventional’ OLS method is its susceptibility to outliers in the data. Elsewhere, we discussed the detection and handling of outliers and gave some broad recommendations.

Discarding observations is generally something that should not be undertaken lightly and needs to be fully justified. This action poses a dilemma for subsequent statistical analysis given the potentially high leverage single aberrant observations may exert on the regression results.

It is with these considerations in mind that alternative regression techniques have been devised that have been shown to be particularly resilient to data abnormalities. These techniques will give results that are in close agreement with classical (OLS) methods when the usual assumptions are satisfied, but differ significantly from the least-squares fit when the errors do not satisfy the normality conditions or when the data contain outliers.

Examples implemented in many common statistical software include:

• robust MM-regression, based on Rousseeuw & Yohai (1984), Yohai & Zamar (1986) and Yohai et al. (1991)
• least trimmed squares (LTS)
• least median squares (LMS)
• least absolute deviations (L1).

Parametric regression can be used when the errors are not normally distributed by improving the estimation procedure. M-estimators (Huber 2009) are a broad class of estimators that includes both the least squares and maximum likelihood estimators. However, in applications, the functional forms of error terms are selected so that the functional values increase more slowly than the original squares of error. The objective function is selected so that, for large error:

r(u) ≤ u²​​
where r is the functional form and u is the error.

An example is the absolute error r(u) ≤ |u| that leads to the median estimator.

Quantile regression

We tend to focus on trends in mean values in data analysis but other attributes of the data may be of interest. For example, climate change may cause only moderate or no change in the mean observed value, but more variation in climate variables (e.g. caused by occurrence of more frequent or extreme flood and drought events) is an indication that quantile values will be more meaningful.

The term ‘quantile’ is synonymous with ‘percentile’, and the best-known example of a quantile is the median value.

Quantile regression was introduced by Koenker & Bassett (1978, 1982) as a way of estimating conditional quantiles in linear regression models. It provides robust inferences as an alternative to the least squares method and does not need to specify an error distribution, which can be difficult in some cases.

Median regression is a special case of quantile regression. While the mean regression uses r(u) = u2 (conventional least square) as its objective function to warrant the conditional expectation of mean, the quantile regression uses:

​
as its objective function, with ρ being the quantile of interest and

being the usual indicator function of the set A.

Quantile regression can be conducted in both parametric and nonparametric settings.

A major drawback with parametric regression approaches is the specification of the regression line. Unless there are strong biophysical reasons that dictate the relationship, you may argue over the choice of parametric form to use as the regression line. While ‘black box’ approaches can be used to examine many regressions and select the best one, nonparametric regression has the advantage of not specifying the regression function. Penalised splines (Hastie & Tibshirani 1990) and regression splines (Wahba 1990) are widely used.

While trend analysis and change detection are important in environmental studies, examination of the effect of other variables provides more insights into environmental condition. For example, many water quality indicators are correlated with flow. If explicitly modelling the relationship between flow and the water quality variables of interest, then regression methods can incorporate exogenous variables.

Time series analysis

Water quality data are observed sequentially in time and are often serially correlated. For example, the concentration of phosphorus in storage at a particular time has a great bearing on the concentration an hour later, and probably a day later. If one measurement is well above the general trend, then the other is likely to be also.

Serial dependence or correlation is particularly evident when the interval between measurements is short (up to monthly) because observations that are close in time have associated unexplained causal effects. An assumption of independence needs to be justified by a diagnostic test or arguments based on knowledge of the process.

A particularly useful tool in identifying and characterising serial dependence is the autocorrelation function (ACF). The ACF is the correlation between pairs of observations separated by a constant lag or time-step.

Pre-whitening is needed before applying rank-based methods or adopting time series methods. As a 2-stage approach, the pre-whitening technique does not work well (Bayazit & Önöz 2007).

Time series analysis, as a branch of statistics, is designed to deal with dependent observations over time. Although not explicitly stated, time series analysis tools try to deal with 4 components:

• (long-term) trend
• seasonal fluctuations (period) with known periodicity
• cyclic nonseasonal variation
• random error by data differentiation and autocorrelation terms (Box & Jenkin 1976).

Autoregressive moving average (ARMA), ARIMA (where ‘I’ stands for integrated) and SARIMA (where ‘S’ stands for seasonal) are extensions of autoregressive (AR) model that include more realistic dynamics by considering autocorrelation in errors, to nonstationarity in mean and seasonality.

The residual serial dependence is often modelled by assuming that it forms an autoregressive process of order ρ, denoted AR(p). This means that the residual εi at time ti depends on the past only through the previous p residuals εi–1, …, εi–ρ. It is often sufficient to assume an AR(1), in which case:

εi = ρεi – 1 + Ʋ_i

where Ʋ_i are assumed to be independent normal random variables and ρ is the lag 1 correlation.

An AR(1) is usually suitable for monthly means but higher-order autoregressive processes may be necessary for more frequent data. Second or higher-order autoregressive processes would imply that the current error has a more complicated dependence on the past. However, longer-term dependence is harder to distinguish from the nonlinear trend.

When the data are collected at irregular intervals, the general approaches are to use approximate timing (e.g. monthly averages) or adopt a continuous AR(1) process. This assumes that the correlation between 2 observations that are d units of time apart is given by ρ^d where ρ is the 1-unit lag correlation (e.g. the correlation between observations that are 1 week apart).

The dependence may also be represented by introducing the lagged response into the regression model as a covariate. This corresponds to an underlying dynamic or differential process and is driven by the (unadjusted) historic water quality in accord with current understanding and hydrological models.

Dealing with autocorrelation

Positive autocorrelation has the important effect of reducing the statistical significance of the estimated time trend. This follows because the effective sample size is smaller when there is significant positive autocorrelation in the data.

An autocorrelation of ρ > 0.2 is sufficient to invalidate the standard errors and confidence intervals obtained using ordinary least squares estimation (Morton 1997). The least squares estimates are generally good estimates but the formal standard errors and confidence intervals can be misleadingly small.

An approximation described in Morton (1997) gives an informal argument suggesting that the standard error for the linear trend component should be multiplied by the factor (refer to Bayley & Hammersley 1946):

The autocorrelation in the regression model is used to describe the short-range structure. However, there is an important confounding between the trend and autocorrelation because both can describe the structure that may exist in the monitoring data.

For example, if the smoothness in the trend component is overestimated, more structure will be ascribed to the autocorrelation and ρ will typically be larger. If too much flexibility is placed in the trend, it may capture some of the local structure than would otherwise be explained by the autocorrelation.

The confounding between autocorrelation and smoothness causes many data-driven methods to choose an inappropriate degree of smoothing. A similar effect is also possible if the structure due to the seasonal component is not adequately estimated.

Autocorrelation complicates water quality trend analyses. The ease with which we can incorporate autocorrelation into the trend analyses depends somewhat on the regression framework.

For linear, polynomial or regression splines (basis splines) approaches, autocorrelation may be readily included when fitted using generalised least squares (GLS). For smoothing splines, Morton & Henderson (2008) found that the traditional GAM software available at the time did not readily allow this, although they suggested that it would be reasonably straightforward to fit this directly. Other more ad hoc approaches for doing this are also used. In the robust regression framework we must assume independence, which is the major limitation with this method.

Most regression methodologies make no assumption about the sampling frequency or intensity. Many of the original advances in water quality trend analysis were generated for monthly monitoring data but carry over naturally to higher or lower-frequency measurements. However, it will become more important to adequately account for the autocorrelation and the fact that observations that are collected closer in time tend to be more alike. Failure to do so may substantially overestimate the effective sample size, underestimate the size of standard errors and result in misleading inferences.

Dealing with data frequency and duration

It is always important to consider the frequency of observations required in relation to what is being detected. For example, if you are looking for trends or changes over several years, then it is probably unnecessary to collect data to the nearest minute. Some form of averaging to a wider time window will have a negligible effect on the information content but may make the interpretation easier and reduce the computational burden.
Irregularly spaced or missing data are naturally accounted for within the general regression framework, although irregularly spaced data usually mean we have to adjust or average the data to a regular time interval, or model the serial correlation using a continuous AR(1) error process. If the proportion of missing data is large, then it may not be possible to estimate the autocorrelation parameter. If the missing data occur in large blocks, then the trend during that period will necessarily be poorly estimated.

The appropriate duration of the monitoring data required will depend on the need and ability to separate effects that are contributing to the data observed at different scales. When strong seasonal components are present, longer sequence lengths are often needed so as to adequately separate the broader general trend from the shorter-term seasonal variation. Longer sequences are also generally needed when there is substantial serial correlation.

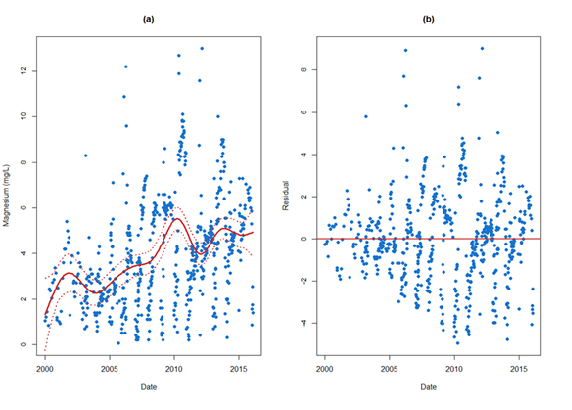
Figure 1a depicts magnesium time series data (from Figure 2 in Data preparation) overlaid with the trend and 95% confidence limits for the fitted curve. While the trend line shown is quite reasonable, care must be exercised when attempting to extrapolate beyond the range of the observed series given the increase in magnesium concentrations. Other features in Figure 1a may also be important, such as the notable increase near the year 2010, which could indicate altered mine practices or different ore-body characteristics.

The variability of a process is equally as important, and sometimes more important than real changes in level.

The definition of variance (Table 2 in Data preparation) is based on departures from the mean (represented as the trend) so any assessment of variation should be performed on the de-trended data. The residuals (original observation minus trend) from this process can be plotted as a separate time series. This has been done for the magnesium data (Figure 1b). Figure 1b shows an apparent change in the process variation beginning in 1993. Further inquiry might determine if this observation was the result of natural or human-induced effects.

Temporal analysis of high frequency monitoring data

It is always important to consider the frequency of observations required in relation to what you are trying to detect. This is particularly important for high-frequency monitoring, which is much more prevalent with the emergence in the market of an array of new sensors for assessing water quality at unprecedented rates.

High-frequency data, however, present new analysis challenges in examining changes over time.

The large volume of data may make any signal difficult to distinguish. This often demands some data summary as part of the analysis, ranging from simple averaging to more sophisticated dimension reduction and exploration through techniques such as Fourier analysis and wavelet analysis.

Driven by an array of new water quality sensors, high-frequency water quality data are increasingly available. It has enormous appeal because it can yield insight into how water quality is changing at resolutions that have not been possible before. Sensors can generate large volumes of data​ that can challenge traditional exploratory methods and create the need for different approaches to the analysis, ranging from the use of simple averaging to reduce the noise in the data to more sophisticated approaches that reduce the dimension in the data.

A variety of smoothing and filtering approaches, such as exponential smoothing approach, autoregressive and moving average linear filtering, Kalman filtering, splines and LOESS (LOcal regrESSion), may be valuable for identifying the signal in a noisy time series dataset. The general intent is to filter out or smooth over some of the high-frequency changes that occur and that may be considered random or unstructured. The smoothed or filtered version is considered to contain the signal, which is what we need to ensure that the sampling frequency enables us to recover.

Different smoothing or filtering methods go about this in different ways and may have different strengths and weaknesses. For instance, some methods may work better when the signal changes fairly smoothly rather than abruptly.

The choice of what is deemed signal and what is considered noise will also vary across methods, and even within a method they will all have different tuning parameters that govern that trade off. For example, the size of the window used in LOESS or the rate parameter in an EMWA. Data-driven methods, such as generalised cross-validation, exist to choose some of these parameters (e.g. spline degrees of freedom).

Spectral and frequency-based time series methods are popular for understanding stationary hydrological or water quality time series amongst a range of applications (Pelletier & Turcotte 1997, Kirchner et al. 2000, Mathevet et al. 2004). For example, the Fourier transform can decompose a time series into a sum of sinusoidal terms of different frequencies. Authors have drawn strong analogies with the signal processing literature and the frequency required to faithfully reproduce a signal.

Others have noted that hydrological time series are often non-stationary, contain intermittent or short-lived features, and involve components that operate or interact at different scales and are not well suited to a Fourier analysis. In these cases, wavelet-based methods offer a significant advantage (Labat 2005, 2010, Kang & Lin 2007, Schaefli et al. 2007, Milne et al. 2009) given their much stronger local focus.

Performing spatial and regional analysis

Spatial modelling and spatiotemporal modelling are important components of an environmental analysis. Measurements are generally taken in both space and time to adequately account for the variability, with the aim of quantifying trends and providing some confidence around the size and significance of that trend.

There are a number of approaches to modelling the underlying processes captured by the data in both space and time.

The first is through what is termed ‘pseudo’ spatiotemporal models, where covariates are included in a modelling framework to capture any space–time dependencies. This can be achieved through a regression modelling framework using a simple linear model or generalised linear model (GLM).

Alternatively, a more flexible model, such as a GAM (Hastie & Tibshirani 1990, Wood 2006), may be more appropriate as the smoothed relationships between the predictor and explanatory variables may be able to explain the spatial or temporal variability in the data, or both. Random effects can be incorporated into these models and therefore represent a generalised additive mixed model (GAMM) (Wood 2006), where an autoregressive structure or autoregressive moving average structures can be explored to accommodate the temporal dependencies in the data.

An example of this type of modelling framework is the work of Kuhnert et al. (2012), where a GAM was used to explore the relationship between water quality constituents and flows and other explanatory terms.

Nonparametric models, such as random forests (outlined in Changes in water quality over time and space), can also be used to capture any spatial and temporal dependencies because the approach considers interactions between a range of variables that may be difficult to structure in a parametric framework, such as a GAM.

An example of random forests being used to model a spatial problem is the work by Kuhnert et al. (2010), who adopted the approach for quantifying gully density in the Burdekin Catchment in Queensland.

The second approach to spatial and or temporal modelling is through an explicit spatial model with random effects that are structured to properly account for the temporal or spatial dependencies, or both. These types of models can vary according to the type of spatial or temporal variation we are trying to accommodate.

For instance, the work of Ver Hoef et al. (2006) focused on developing spatial models for stream networks where a variety of correlation structures were considered to take into account the direction of flow through a stream network. Cressie (1993) and Banerjee et al. (2004) constructed spatial random effects models to take into account spatial correlation. The structure of these random effects can be tailored to accommodate points in space, gridded data or broader spatial structures.

The space–time modelling outlined in Cressie & Wikle (2011) tackles dependencies in space and time within a Bayesian framework by structured selection of basis functions. These basis functions, which may or may not be orthogonal, approximate the spatial and temporal elements of the processes being modelled to make estimation easier, particularly for large and complex datasets.

References

Banerjee S, Carlin BP & Gelfand AE 2004, Hierarchical Modeling and Analysis for Spatial Data, Chapman and Hall/CRC, Boca Raton.

Bayazit M & Önöz B 2007, To prewhiten or not to prewhiten in trend analysis? Hydrological Sciences Journal 52: 611–624.

Bayley GV & Hammersley JM 1946, The “effective” number of independent observations in an autocorrelated time series, Supplement to the Journal of the Royal Statistical Society 8: 184–197.

Box GEP & Jenkins GM 1976, Time Series Analysis: Forecasting and control, 2nd Edition, Holdon-Day, San Francisco.

Brillinger DR 1994, Trend analysis: time series and point process problems, Environmetrics 5: 1–19.

Brockwell P & Davis R, 2016, Introduction to Time Series and Forecasting, 4th Edition, Springer, New York.

Chatfield C 2003, The Analysis of Time Series: An introduction, 6th Edition, CRC Press, Boca Raton.

Cleveland WS 1979, Robust locally weighted regression and smoothing scatterplots, Journal of the American Statistical Association 74: 828–836.

Cressie NAC 1993, Statistics for Spatial Data, Revised Edition, John Wiley and Sons, New York.

Cressie N & Wikle CK 2015, Statistics for Spatio-Temporal Data, Wiley, New Jersey.

Esterby SR 1996, Review of methods for the detection and estimation of trends with emphasis on water quality applications, Hydrological Processes 10: 127–149.

Gallant AR & Fuller WA 1973, Fitting segmented polynomial regression models whose join points have to be estimated, Journal of the American Statistical Association 68(1): 144–147.

Gilbert RO 1987, Statistical Methods for Environmental Pollution Monitoring, Van Nostrand Reinhold, New York.

Hastie TJ & Tibshirani RJ 1990, Generalized Additive Models, Chapman and Hall/CRC, London.

Helsel D & Hirsch RM 1992, Statistical Methods in Water Resources, Volume 49, Elsevier, Amsterdam.

Henderson BL & Morton R 2008, Strategies for the estimation and detection of trends in water quality, report 07/70, CSIRO Water for Healthy Country Flagship, Canberra.

Huber PJ 2009, Robust Statistics, 2nd Edition, John Wiley & Sons, Hoboken.

Kang S & Lin H 2007, Wavelet analysis of hydrological and water quality signals in an agricultural watershed, Journal of Hydrology 338(1–2): 1–14

Kendall M 1938, A new measure of rank correlation, Biometrika 30: 81–89.

Kirchner J, Feng X & Neal C 2000, Fractal stream chemistry and its implications for contaminant transport in catchments, Nature 403: 524–527.

Koenker R & Bassett G 1978, Regression quantiles, Econometrica 46: 33–50.

Koenker, R & Bassett G 1982, Robust tests of heteroscedasticity based on regression quantiles, Econometrica 50: 43–61.

Kuhnert PM, Henderson A-K, Bartley R & Herr A 2010, Incorporating uncertainty in gully erosion calculations using the Random Forests modelling approach, Environmetrics 21: 493–509.

Kuhnert PM, Henderson B, Lewis SE, Bainbridge ZT, Wilkinson S & Brodie JE 2012, Quantifying total suspended sediment export from the Burdekin River catchment using the loads regression estimator tool, Water Resources Research 48(4): 1–18.

Labat D 2005, Recent advances in wavelet analyses: Part 1. A review of concepts, Journal of Hydrology 314(1–4): 275–288.

Labat D 2010, Cross wavelet analyses of annual continental freshwater discharge and selected climate indices, Journal of Hydrology 385: 269–278.

Mathevet T, Lepiller M & Mangin A 2004, Application of time-series analyses to the hydrological functioning of an Alpine karstic system: the case of Bange-L’Eau-Morte, Hydrology and Earth System Science 8: 1051–1064.

Miller JD & Hirst D 1998, Trends in concentrations of solutes in an upland catchment in Scotland, Science of the Total Environment 216: 77–88.

Milne A, Macleod C, Haygarth P, Hawkins J & Lark R 2009, The wavelet packet transform: A technique for investigating temporal variation of river water solutes, Journal of Hydrology 379(1–2): 1–19.

Morton R 1997, Semi-parametric models for trends in stream salinity, report no. CMIS 97/71, CSIRO Mathematical and Information Sciences, Canberra.

Morton R & Henderson B 2008, Estimation of nonlinear trends in water quality: An improved approach using generalized additive models, Water Resources Research 44(7): W07420.

Nadaraya EA 1964, On estimating regression, Theory of Probability and its Applications 9(1): 141–2.

Pelletier J & Turcotte, D 1997, Synthetic stratigraphy with a stochastic diffusion model of fluvial sedimentation, Journal of Sedimentary Research, Section B: Stratigraphy and Global Studies 67(6), 1060–1067.

Pettitt AN 1979, A non-parametric approach to the change-point problem, Applied Statistics 28(2): 126–135.

Robson AJ & Neal C 1996, Water quality trends at an upland site in Wales, UK, 1983–1993, Hydrological Processes 10: 183–203.

Rousseeuw PJ & Yohai VJ 1984, Robust regression by means of S-estimators, Robust and Nonlinear Time Series Analysis pp. 256–272, Lecture Notes in Statistics 26.

Schaefli B, Maraun D, & Holschneider M 2007, What drives high flow events in the Swiss Alps? Recent developments in wavelet spectral analysis and their application to hydrology, Advances in Water Resources 30(12): 2511–2525.

Schreider SY, Jakeman AJ, Letcher RA, Nathan RJ, Neal BP & Beavis SG 2002, Detecting changes in streamflow response to changes in non-climatic conditions: farm dam development in the Murray–Darling basin, Australia, Journal of Hydrology 262(1–4): 84–98.

Shao Q & Campbell NA 2002, Applications: Modelling trends in groundwater levels by segmented regression with constraints, Australian and New Zealand Journal of Statistics 44: 129–141.

Shumway R & Stoffer D 2006, Time Series Analysis and Its Applications, 4th Edition, Springer, New York.

Spearman C 1904, The proof and measurement of association between two things, American Journal of Psychology 15: 72–101.

Ver Hoef JM, Peterson EE & Theobald D 2006, Spatial statistical models that use flow and stream distance, Environmental and Ecological Statistics 13 449–464.

Wahba G 1990, Spline Models for Observational Data, SIAM, Philadephia.

Ward RC, Loftis JC & McBride GB 1990, Design of Water Quality Monitoring Systems, VanNostrand Reinhold, New York.

Watson GS 1964, Smooth regression analysis, Sankhyā: The Indian Journal of Statistics, Series A 26 (4): 359–372.

Wood S 2017, Generalized Additive Models: An introduction with R, Chapman and Hall/CRC, Florida.

Yohai VJ, Stahel WA & Zamar RH 1991, A procedure for robust estimation and inference in linear regression, in: Stahel WA & Weisberg S (eds), Directions in Robust Statistics and Diagnostics, The IMA Volumes in Mathematics and its Application, vol. 34, Springer, New York.

Yohai VJ & Zamar R 1986, High breakdown-point estimates of regression by means of the minimization of an efficient scale, Journal of the American Statistical Association 83: 406–413.